precautions in specific heat capacity experiment

What are the precautions in specific heat capacity experiment?

There are several precautions that should be taken in specific heat capacity experiments:

• The sample should be of a known, uniform composition.
• The sample should be of a known, uniform size.
• The sample should be of a known, uniform shape.
• The sample should be clean and dry.
• The sample should be at the same temperature as the calorimeter.
• The calorimeter should be well insulated.
• The calorimeter should be of known heat capacity.
• The surroundings should be at a constant temperature.

David Denton ∙

Some precautions to consider in a specific heat capacity experiment include ensuring that the equipment is calibrated correctly, using an appropriate amount of the substance being tested, maintaining a consistent temperature throughout the experiment, and taking proper safety measures when handling hot objects or substances.

Add your answer:

What is the precaution taken on specific heat capacity experiment?

Some precautions taken during a specific heat capacity experiment include ensuring the apparatus is properly calibrated, using consistent and accurate measurements, minimizing heat loss to the surroundings, and maintaining a controlled environment to reduce external influences on the results. These precautions help ensure the accuracy and reliability of the data collected during the experiment.

What are precaution in specific heat capacity experiment?

Some precautions to consider in a specific heat capacity experiment include ensuring proper insulation to minimize heat loss, using accurate measuring instruments to determine mass and temperature changes, and conducting the experiment in a controlled environment to avoid external influences on the results. Additionally, it's important to handle hot objects with care and follow appropriate safety protocols when working with heat sources.

To determine the specific heat capacity of a solid conclusion?

To determine the specific heat capacity of a solid, conduct an experiment where you measure the temperature change of a known mass of the solid when a known amount of heat is added or removed. By calculating the specific heat capacity using the formula Q = mcΔT (where Q is the heat energy, m is the mass, c is the specific heat capacity, and ΔT is the temperature change), you can determine the specific heat capacity of the solid. Repeat the experiment multiple times to ensure accuracy and reliability in your conclusion.

Why does the temperature of the metal fall from its maximum after a while in a specific heat capacity of metals experiment?

The temperature of the metal falls from its maximum during a specific heat capacity experiment because the metal is losing heat to its surroundings through conduction and radiation. This heat loss causes the temperature to decrease over time until it reaches equilibrium with the surrounding environment.

How do you reduce the errors in specific heat capacity experiment?

To reduce errors in a specific heat capacity experiment, ensure proper calibration of equipment, accurately measure mass and temperature, minimize heat loss through insulation, and repeat measurements to calculate an average. Additionally, use a consistent method and ensure the substance is uniform to improve accuracy.

What is the conclusion on specific heat capacity of liquid experiment?

The conclusion of an experiment on specific heat capacity of a liquid would typically summarize the findings regarding how much heat energy is required to raise the temperature of a unit mass of the liquid by one degree Celsius. It may also discuss any trends or patterns observed, the accuracy of the results obtained, and compare the experimental value to known literature values for specific heat capacity.

What is the independent variable in the calorimeter and specific heat experiment?

The independent variable in a calorimeter and specific heat experiment is typically the type of material being tested. By changing the type of material used in the experiment, one can examine how the specific heat capacity of different materials affects the amount of heat absorbed or released during a reaction.

What factor most influence the amount of energy needed to change the temperature of a substance?

specific heat capacity

What is the specific heat capacity of Polyester?

The specific heat capacity of polyester is 2.35degrees

Why should you stir the water at the end of the experiment specific heat capacity?

Stirring the water at the end of the experiment helps ensure that the temperature throughout the water is uniform, which is important for accurate measurements of specific heat capacity. It helps to distribute the heat evenly and eliminate any temperature gradients that may affect the results.

Which metal has the highest specific heat capacity?

No. Metals have a relatively low specific heat.

What is the conclusion of specific heat capacity experiment?

Normally you'd say something about the heat of formation. Exactly what that would be depends on the results you got, which we obviously don't know.

Top Categories

• CBSE Class 11
• CBSE Class 11 Physics Practical
• To Determine Specific Heat Capacity Of A Given Solid By Method Of Mixture

To Determine Specific Heat Capacity of a Given Solid by Method of Mixture

Specific heat capacity is defined as the amount of heat required for one gram of substance at 1℃. To understand how to determine the specific heat capacity of a given solid by the method of mixtures, please read the below article.

To determine the specific heat capacity of a given solid by the method of mixtures.

Materials Required

• A hypsometer
• Calorimeter
• A lid and outer jacket
• Solid in small pieces
• Two half-degree thermometers
• Clamp stand

The calorimeter is a device used to measure the heat flow of a chemical or physical reaction. Calorimetry is the process of measuring this heat. It consists of a metal container to hold water above the combustion chamber and a thermometer to measure the temperature change. Hypsometer is an instrument used to determine the boiling point of water at a given altitude.

• Put thermometers A and B in a beaker containing water and note their reading. Let thermometer A be a standard to find the correction that is to be applied to thermometer B.
• Put the thermometer B into the copper tube of a hypsometer containing the powder of the given solid. Before placing the hypsometer on the burner, add a sufficient amount of water.
• Record the weight of the calorimeter with a stirrer and lid over it.
• Add water (temperature between 5 to 8℃) to the calorimeter at half-length and weigh it again.
• Heat the hypsometer till the temperature of the solid is steady.
• Note the temperature of water in calorimetry. Now slowly stir and add the solid powder from the hypsometer to the calorimeter and record the final temperature of the mixture.
• Remove thermometer A from the calorimeter.
• Note the weight of the calorimeter with the contents and lid.

Observations

Reading of thermometer A = T A = ……… ℃

Reading of thermometer B = T B = ……… ℃

Correction applied in B with respect to A (T A – T B ) = …….. ℃

Mass of calorimeter and stirrer m = …….. g

Water equivalent of calorimeter ω = m × 0.095 = …….. g

Specific heat of copper calorimeter = 0.095 cal/g

Mass of calorimeter + stirrer + lid = m 1 = ……. g

Mass of calorimeter + stirrer + lid + cold water = m 2 = …… g

The steady temperature of hot solid = T s = …….. ℃

Corrected temperature of hot solid T =T s – (T A – T B ) = ……… ℃

The temperature of cold water = t =……… ℃

The temperature of the mixture = Ө =…….. ℃

Mass of calorimeter, stirrer, lid, cold water, and solid = m 3 =…… g

Calculations

Mass of cold water = m 2 – m 1 =…….. g

Mass of hot solid = m 3 – m 2 =…….. g

Rise of the temperature of cold water and calorimeter = Ө – t =………. ℃

Fall in temperature of solid = T – Ө =……… ℃

Heat gain by calorimeter, cold water and stirrer = [ω + ( m 2 – m 1 )(Ө – t)] =……. (a)

Heat lost by solid = (m 3 – m 2 ) × C × (T – Ө) =……. (a)

Here, C is the specific heat of solid to be calculated.

According to the principle of calorimeter, heat lost = heat gained

Specific heat of given solid by the method of the mixture is ………. cal g -1 ℃ -1 .

Precautions

• A sufficient amount of solid powder should be used to cover the tip of the thermometer.
• A sufficient amount of water should be taken in a hypsometer.
• Dropping of solid should be quick and gentle.
• To avoid excess radiation, the calorimeter should be polished from the outside.
• The temperature of cold water should not cross the dew point.

Sources of Error

• There might be heat loss while transferring solid into the calorimeter.
• During conduction, convection, and radiation, there might be heat loss.
• The bulbs of the thermometer might not be completely inside the solid.

Note: To determine the specific heat of a given liquid by the method of mixtures, the liquid is taken in place of cold water to determine the specific heat. Proceed with the same procedure as in the experiment.

Q1. What is the heat?

Ans: Heat is defined as the quality of being hot at high temperatures.

Q2. Define the specific heat of the substance.

Ans: It is defined as the amount of heat energy required to raise the temperature of 1 gram of a substance by 1℃.

Q3. State the principle of calorimetry.

Ans: The principle of calorimetry is heat lost is equal to the heat gained.

Q4. Why is calorimeter made of copper is used in the experiment?

Ans: The specific heat of copper is very low. The absorption and liberation of heat will be less during heat transfer.

Q5. Is heat gained always equal to the heat lost?

Ans: If there is no chemical reaction taking place between the components only then heat loss will be always equal to the heat gain.

Stay tuned with BYJU’S to learn more about other Physics related experiments.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

Request OTP on Voice Call

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Specific Heat Capacity Experiment

The specific heat capacity of a substance is the amount of energy needed to increase the temperature of 1 kg of that substance by 1°C.

Increasing internal energy of the body

• The heater increases the internal energy of the body and we measure this using a joulemeter.

Measuring the body's temperature

• Measure the temperature of the body (object) at the start and measure the maximum temperature of the body at the end.

Calculating specific heat capacity

• Specific heat capacity = c h a n g e    i n    i n t e r n a l    e n e r g y m a s s    ( k g )    ×    m a x i m u m    t e m p e r a t u r e    r i s e    ( o C ) \frac{change \;in\; internal\; energy}{mass \;(kg)\; {\times}\; maximum \;temperature\; rise\; (^oC)} ma ss ( k g ) × ma x im u m t e m p er a t u re r i se ( o C ) c han g e in in t er na l e n er g y ​

1.1 Energy Changes

1.1.1 Energy Stores

1.1.2 Energy Storing

1.1.3 Internal Energy

1.1.4 Kinetic Energy Storage

1.1.5 Gravitational Potential Energy Storage

1.1.6 Elastic Potential Energy Storage

1.1.7 Calculating Changes in Energy

1.1.8 Changes in Kinetic Energy - Calculations

1.1.9 Changes in GPE - Calculations

1.1.10 Changes in EPE - Calculations

1.1.11 Energy Transfers

1.1.12 Energy Transfer Examples

1.1.13 Mechanical Work Done

1.1.14 Mechanical Work Done Equation

1.1.15 Mechanical Work - Calculations

1.1.16 Electrical Work Done

1.1.17 Power

1.1.18 Electrical Work Done- Calculations

1.2 Energy Losses & Efficiency

1.2.1 Energy Wastage

1.2.2 Efficiency

1.2.3 Reducing Energy Loss

1.2.4 Power & Energy Transfer

1.2.5 Efficiency - Calculations

1.2.6 Grade 9 - Energy & Efficiency

1.3 Energy Resources

1.3.1 Energy Resources

1.3.2 Fossil Fuels

1.3.3 Geothermal Energy

1.3.4 Wind Energy

1.3.5 Water Energy

1.3.6 Tidal Energy

1.3.7 Nuclear Energy

1.3.8 Solar Energy

1.3.9 Original Source of Energy

1.3.10 Non-Renewable and Renewable Resources

1.3.11 Uses of Energy Sources

1.3.12 Changing Electricity Use

1.3.13 Renewable Energy

1.3.14 End of Topic Test - Energy

1.3.15 Exam-Style Questions - Energy

2 Electricity

2.1 Electric Charge

2.1.1 Circuit Diagrams

2.1.2 Circuit Symbols

2.1.3 Current

2.1.4 Current Equation

2.1.5 Current - Calculations

2.1.6 Conductors

2.1.7 Potential Difference

2.1.8 Voltage Equation

2.1.9 Measurements in Circuit

2.1.10 Voltage - Calculations

2.2 Resistance & Electrical Work

2.2.1 Resistance

2.2.2 Resistance Graph

2.2.3 Diodes

2.2.4 LDRs and Thermistors

2.2.5 Electrical Work

2.2.6 Power

2.2.7 Ohm's Law

2.2.8 Resistance and Ohms Law - Calculations

2.2.9 Electrical Work - Calculations

2.3 Electric Circuits

2.3.1 Series Circuits

2.3.2 Resistors

2.3.3 Cells

2.3.4 Potential Difference

2.3.5 Series Circuits - Calculations

2.3.6 Parallel Circuits

2.3.7 Parallel Current

2.3.8 Parallel Resistance

2.3.9 Lights in Parallel

2.3.10 Parallel Circuits - Calculations

2.3.11 Grade 9 - Circuits

2.3.12 Exam-Style Questions - Electricity

2.4 Electricity in Homes

2.4.1 AC/DC

2.4.2 Mains Electricity

2.4.3 Power Ratings

2.4.4 National Grid

2.4.5 Domestic Uses - Calculations

2.4.6 Fuses & Circuit Breakers

2.4.7 Earthing

2.4.8 Dangers of the Live Wire

2.4.9 End of Topic Test - Electricity

2.5 Static Electricity

2.5.1 Electrical Charge

2.5.2 Charging an Object

2.5.3 Charged Objects

2.5.4 Static Electricity

2.5.5 Electric Fields

3 Particle Model of Matter

3.1 States of Matter

3.1.1 Atomic Model

3.1.2 Atomic Structure

3.1.3 Sub-Atomic Particles

3.1.4 Models of the Atom

3.1.5 Alpha Particles

3.1.6 Electron Arrangements

3.1.7 Density

3.1.8 Density Equation

3.1.9 Density and the Particle Model

3.1.10 Density - Calculations

3.1.11 Changes of State

3.1.12 Exam-Style Questions - Density

3.2.1 Internal Energy

3.2.2 Change in Thermal Energy

3.2.3 Specific Heat Capacity Experiment

3.2.4 Equation for Heat Capacity

3.2.5 Leslie's Cube

3.2.6 Internal Energy - Calculations

3.2.7 Melting and Boiling

3.2.8 Latent Heat

3.2.9 Energy Change for Change of State

3.2.10 Latent Heat - Calculations

3.2.11 Latent Heat Experiments

3.3 Particle Motion in Gases

3.3.1 States of Matter

3.3.2 Properties of Gases

3.3.3 Temperature Increase in a Gas

3.3.4 Work Done on a Gas

3.3.5 End of Topic Test - Particle Model of Matter

3.3.6 Grade 9 - Particle Model of Matter

3.3.7 Exam-Style Questions - Specific Heat Capacity

4 Atoms & Radiation

4.1.1 Atomic Model

4.1.2 Structure of an Atom

4.1.3 Sub-Atomic Particles

4.1.4 Alpha Particles

4.1.5 The Model of the Atom

4.1.6 Electron Arrangements

4.1.7 Proton and Nucleon

4.1.8 Atoms and Ions

4.1.9 Isotopes

4.1.10 Carbon Nuclides

4.1.11 Exam-Style Questions - Atomic Structure

4.2 Radiation

4.2.1 Radioactivity

4.2.2 Types of Radiation

4.2.3 Detection

4.2.4 Background Radiation

4.2.5 Types of Radioactive Emission

4.2.6 Ionising vs Penetration

4.2.7 Practical Applications of Radiation

4.2.8 Nuclear Fission

4.2.9 Nuclear Fusion

4.2.10 Radioactive Decay

4.2.11 Radioactive Decay Equations

4.2.12 Fission & Fusion Equations

4.2.13 Radio. decay equations - Calculations

4.2.14 Half Lives

4.2.15 Measuring Half Lives

4.2.16 Ionising Radiation

4.2.17 Half Life -Calculations

4.2.18 Safety Precautions

4.2.19 Uses for Isotopes With Different Half-lives

4.2.20 Radioactive Contamination and Irradiation

4.2.21 Peer Review

4.2.22 End of Topic Test - Atoms & Radiation

4.2.23 Grade 9 - Radiation

4.2.24 Exam-Style Questions - Radioactive Decay

5.1 Basics of Motion

5.1.1 Velocity

5.1.2 Average Speed

5.1.3 Adding Vectors

5.1.4 Acceleration

5.1.5 Distance vs Displacement

5.1.6 Contact and Non-Contact Forces

5.1.7 Distance-Time Graphs

5.1.8 Speed-Time Graphs

5.1.9 Average Speed - Calculations

5.1.10 Acceleration - Calculations

5.1.11 Uniform Acceleration - Calculations

5.1.12 Grade 9 - Motion

5.1.13 Exam-Style Questions - Motion

5.2.1 Mass and Inertia

5.2.2 Weight

5.2.3 Centre of Mass

5.2.4 Gravity - Calculations

5.2.5 Resultant Forces

5.2.6 Newton's First Law

5.2.7 Newton's Third Law

5.2.8 Newton Second Law - Calculations

5.2.9 Free Body Force Diagrams

5.2.10 Components of Forces

5.2.11 Free Body Diagrams - Calculations

5.2.12 Stretching a Spring

5.2.13 Hooke's Law and Equation

5.2.14 Spring Experiment

5.2.15 Hooke's Law - Calculations

5.2.16 Elastic Potential Energy

5.2.17 Elastic Potential - Calculations

5.2.18 Exam-Style Questions - Elastic Potential Energy

5.3 Effects of Forces

5.3.1 Acceleration

5.3.2 Air Resistance and Friction

5.3.3 Graphing Acceleration

5.3.4 Momentum

5.3.5 Momentum: Law of Conservation

5.3.6 Force and Momentum Change

5.3.7 Change in Momentum - Calculations

5.3.8 Momentum - Calculations

5.3.9 Moments

5.3.10 Equilibrium

5.3.11 Moments - Calculations

5.3.12 Circular Motion

5.3.13 Levers & Gears

5.3.14 Stopping Distance

5.3.15 Factors Affecting Stopping Distance

5.3.16 Decelerations

5.3.17 Stopping Distance - Calculations

5.4 Pressure

5.4.1 Pressure & Force on Container

5.4.2 Atmospheric Pressure

5.4.3 Liquid Pressure

5.4.4 Pressure - Calculations

5.4.5 Liquid Pressure - Calculations

5.4.6 Upthrust

5.4.7 Pressure Difference

5.4.8 End of Topic Test - Forces

5.4.9 Exam-Style Questions - Pressure

6.1 Wave Basics

6.1.1 Wave Basics

6.1.2 Wave Speed Formula

6.1.3 Wave Speed Equation

6.1.4 Wave Speed - Calculations

6.1.5 Wave Frequency Formula

6.1.6 Wavelength and Amplitude

6.1.7 Wave Frequency - Calculations

6.1.8 Transverse Waves

6.1.9 Longitudinal Wave

6.1.10 Required Practical - Ripple Tank

6.2 Waves at a Boundary

6.2.1 Waves at a Boundary

6.2.2 Reflection of Light

6.2.3 Refraction of Light

6.2.4 Internal Reflection

6.3 Sound Waves

6.3.1 Sound Waves

6.3.2 Sound Waves and our Ears

6.3.3 Speed of Sound

6.3.4 Speed of Sound Experiment

6.3.5 Sound as a Wave

6.3.6 Uses of Sound Waves: Ultrasound Waves

6.3.7 Uses of Sound Waves: Earthquakes

6.3.8 Sound Waves - Calculations

6.3.9 End of Topic Test - Introduction to Waves

6.3.10 Exam-Style Questions - Wave Speed

6.4 Electromagnetic Waves

6.4.1 Properties

6.4.2 Gamma Rays

6.4.3 X-Rays

6.4.4 UV Light

6.4.5 Infrared Radiation

6.4.6 Microwaves

6.4.7 Radio Waves

6.4.8 Properties 2

6.4.9 Visible Light

6.4.10 Specular and Diffuse Reflection

6.4.11 Colours

6.4.12 Grade 9 - Waves

6.5.1 Lenses

6.5.2 Convex Lens

6.5.3 Concave Lens

6.5.4 Lenses - Calculations

6.5.5 Images

6.5.6 Ray Diagrams

6.6 Heat & Radiation

6.6.1 Infrared Radiation

6.6.2 Radiation & Surface Colour

6.6.3 Surface Area & Temperature

6.6.4 Temperature

6.6.5 Greenhouse Effect

6.6.6 Energy Balance of the Earth

6.6.7 End of Topic Test - EM Waves, Lenses & Heat

6.6.8 Exam-Style Questions - EM Radiation

7 Magnetism

7.1 Magnetism Basics

7.1.1 Magnetism

7.1.2 Magnetic Materials

7.1.3 Induced Magnetism

7.1.4 Magnetic Fields

7.1.5 Magnetic Field Patterns

7.2 Electromagnetism

7.2.1 The Magnetic Effect of a Current

7.2.2 Solenoid Field

7.2.3 Magnetic Field Strength

7.2.4 Uses of Electromagnets

7.2.5 Motor Effect

7.2.6 Magnetic Flux Equation

7.2.7 Magnetic Flux - Calculations

7.2.8 Electric Motors

7.2.9 Force Acting on a Coil in a Magnetic Field

7.2.10 Induced Potential Difference

7.2.11 Magnetic Field Direction

7.2.12 Forces Between Electricity and Magnets

7.2.13 AC/DC

7.2.14 Generator Effect

7.3 Transformers

7.3.1 Transformers

7.3.2 Transformer Equation

7.3.3 Step-Up and Step-Down Transformers

7.3.4 Principles of Transformer Operation

7.3.5 High-Voltage Transmission and Transformers

7.3.6 Energy in Transformers

7.3.7 Power Losses in Cables

7.3.8 Transformers - Calculations

7.3.9 Transformers 2 - Calculations

7.3.10 End of Topic Test - Magnetism

7.3.11 Grade 9 - Transformers

7.3.12 Exam-Style Questions - Magnetic Fields

8 Astrophysics

8.1 Astrophysics

8.1.1 The Solar System

8.1.2 The Sun

8.1.3 The Solar System - Calculations

8.1.4 Orbits

8.1.5 Stable Orbits

8.1.6 Orbits HyperLearning

8.1.7 Life Cycle of a Star

8.1.8 Creation of Elements

8.1.9 Red-shift

8.1.10 The Big Bang Theory

8.1.11 Gaps in Knowledge

8.1.12 End of Topic Test - Astrophysics

8.1.13 Exam-Style Questions - Astrophysics

Jump to other topics

Unlock your full potential with GoStudent tutoring

Affordable 1:1 tutoring from the comfort of your home

Tutors are matched to your specific learning needs

30+ school subjects covered

Change in Thermal Energy

Equation for Heat Capacity

Absolute vs Direct Thermal Conductivity

May 3, 2024

Thermal Conductance Calculator

July 7, 2022

Thermal Conductivity & Thermal Resistance Calculator

June 24, 2022

Chasing Rainbows

January 24, 2022

Efim Litovsky

October 28, 2021

Top 10 Thermally Conductive Materials

July 8, 2019

Conduction Calculator

September 22, 2017

What is Thermal Conductivity?

November 26, 2018

Thermal Conductivity Meter: Lee’s Disc

June 9, 2017

Materials Database

September 27, 2017

Uncertainty of Calibration

July 24, 2017

Rule of Mixtures Calculator

January 30, 2019

Specific Heat Test Experiment

1.0 introduction.

When performing an experiment and carefully following the proper procedure methods, the results obtained should be relatively accurate. Many experiments require multiple trials and sometimes never result in a complete conclusion.

The specific heat test described in this article required many modifications and repetitions to display conclusive results. The results obtained were relatively accurate even taking into consideration the modification of using a calorimeter made of Styrofoam cups. Often results from experiments using modifications can be inaccurate or inconclusive, especially when there is only a single recorded data point. In this article we will go through proper data acquisition and analysis.

When using proper procedure for this in-home experiment, it is unlikely that 100% accuracy will be achieved due to the unstoppable nature of thermodynamics. Following this method can give an accuracy of approximately 80%. This is a respectable degree of accuracy to be achieved from a simple DIY application.

2.0 Procedure

The procedure for this experiment is thoroughly covered in the coinciding Specific Heat Test article. A brief summary of the procedure is outlined below.

A mass of water was measured than poured into the calorimeter, the water remained there until it reached room temperature. For the most accurate and readable results, there should only be enough water in the calorimeter to completely cover the sample.

Figure 1: Calorimeter made of two Styrofoam cups and a thermometer

A beaker filled with approximately 300mL of water was placed on a hot plate. A sample of the stainless-steel variety used for the purpose of this experiment was then placed in a test tube and set in a stand so that the majority of the tube was submerged in the beaker. The sample tube was placed vertically to ensure that it did not come into contact with the bottom or sides of the beaker. Once the sample tube was placed properly; the hot plate was turned on.

Figure 2: Beaker on a hot plate with a test tube containing the sample submerged in boiling water

During the initial trial of this experiment a solid 25.22-gram cylindrical stainless-steel-316 sample was used. Using a test tube to hold the sample in the water (as shown above), did not lead to favorable results. This poor experimental outcome is likely due to the sample’s radius being smaller than the radius of the test tube. This additional space around the sample added a layer of insulating air in the test tube. This error could be averted if the sample were a powder or composed of smaller pieces.

However, if changes were made to the sample at this point in the experiment, the sample would be completely destroyed. For the remainder of the experiment the sample was held in place with a pair of insulated tongs instead of the test tube. Altering this element of the procedure for the remainder of the trials dramatically improved the results.

Figure 3: Beaker on a hot plate with a sample submerged and hovered above the bottom by tongs

Once the water in the beaker was boiling, it was recommended to wait approximately 10 minutes to ensure the sample is evenly heated. Note that to achieve a boiling condition the sample needs to be heated to 100 degrees Celsius.

2.3 Material Transfer

After 10 minutes the test tube was detached from the stand and the sample was poured into the calorimeter. The sample must be poured safely but quickly into the calorimeter, so that a minimal amount of heat is lost to the surrounding air. It is also crucial not to transfer any water from the beaker into the calorimeter. If water from the beaker entered the calorimeter in would add heat that is unrelated to the sample and alter the calculated mass of water.

A Styrofoam cup calorimeter was used for the first two trials of this experiment. For the third and fourth trials a metal thermos replaced the Styrofoam cups to determine the difference a conductive material had on the results.

Figure 4: A Calorimeter made from a thermos and a digital thermometer

2.4 Record Data

Once the sample was stabilized in the enclosed calorimeter, data was collected from the thermometer. For the purposes of this experiment, data was recorded at every 30 second interval. However, this experiment is not time sensitive so depending on the conditions, data can be reordered at multiple different intervals. Data was continuously recorded until the temperature of the substance started to drop indicating that the highest possible temperature was achieved.

Recording temperatures at intervals is the recommended option compared to just waiting for the temperature peak. Having a consistent recording time ensures the most accurate results and minimalizes chances for error.

3.0 Analyzing your Data

3.1 a preliminary look.

The data obtained from the temperature analysis was entered into Microsoft excel (any program would suffice). Using Microsoft excel the data was placed into a graph format for easy comparison between trials. The graphs produced from the data would indicate any errors that could have possibly occurred during the experimental trials. If errors are observed the experiment would have to be repeated before continuing further analysis.

Acceptable data will display a noticeable curve in the graph indicating the relationship between temperature and time. Additional modifications that could be implemented to improve results could be breaking the sample into smaller pieces, having a larger mass of sample or having less water in the calorimeter. All of these would impact the deviation in the temperature difference displaying more drastic changes in temperature. Increased variation would make the results more noticeable and the data calculations would also be more accurate.

3.2 A Deeper Look

The time that the peak temperature occurred is displayed noticeably in the graphs of the experimental data. Depending on the compatibility of the data with the software being used for the analysis a line of best fit can be produced from the peak temperature. Errors bars are optional depending on the purpose of the experiment and the results obtained. The majority of the error in the results would be due to the unpreventable loss of heat to the air and the calorimeter.

3.3 Results

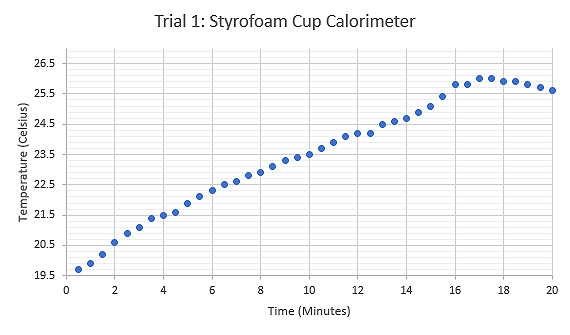
Figure 5: Graph displaying the relationship between Temperature (°C) and Time (minutes) during the first trial using a Styrofoam cup calorimeter and heated sample test tube

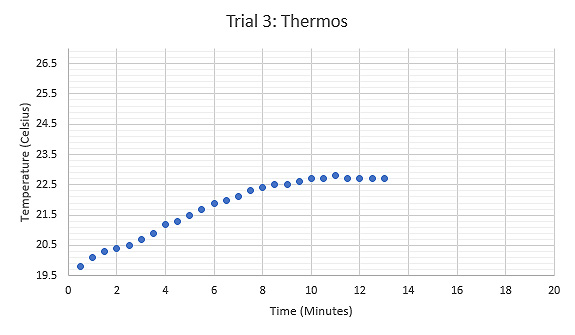
Figure 7: Graph displaying the relationship between Temperature (°C) and Time (minutes) during the third trial using a thermos as the calorimeter, tongs held the sample while heated.

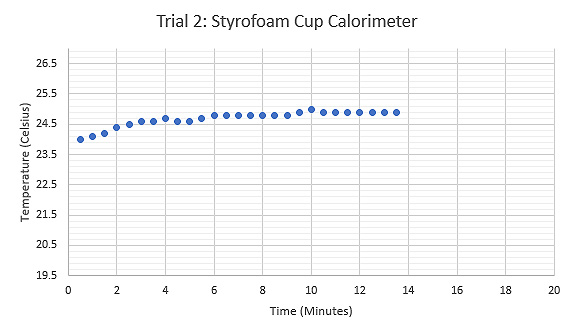
Figure 6: Graph displaying the relationship between Temperature (°C) and Time (minutes) during the second trial using a Styrofoam cup, tongs held the sample while heated.

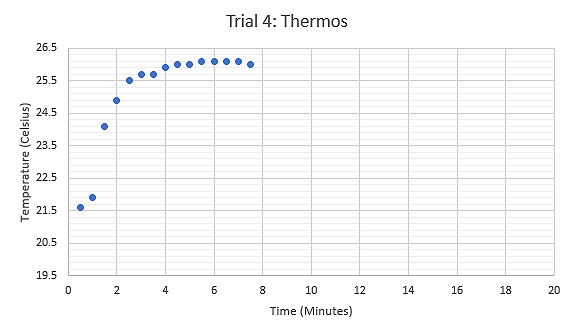
Figure 8: Graph displaying the relationship between Temperature (°C) and Time (minutes) during the fourth trial using a thermos at room temperature as the calorimeter, tongs held the sample while heated.

(Note that the ideal form of a graph of temperature change versus time due to a gradient would be logarithmic.)

3.4 Calculations

The first law of thermal dynamics states that all energy in the universe is conserved. This law can be applied to the results from the experiment. When the sample cools down, energy is lost in the form of heat. As the law states, this energy doesn’t just disappear, in the case of this experiment that energy is absorbed by the water. This increase in energy will cause the water’s temperature to rise. Measuring this change determines the amount of heat absorbed by the water which leads to determining the heat lost by the stainless-steel sample.

Q w = -Q s    Where Q is the change in heat.

Using specific heat of water and the mass of water being used, we can express the above more informatively.

Q w = c w m w (T peak – T initial ) w = -Q s = c s m s (T peak – T initial ) s

The formula can then be rearranged for determining the specific heat of the sample.

c s = c w m w ΔT w / m s ΔT s

3.5 Discussing Results

For the first trial of the experiment, Styrofoam cups were used as the calorimeter along with a test tube for holding the sample. The results from this trial were inconclusive and had a large amount of error. In the second trial a pair of insulated tongs replaced the test tube for holding the sample. The results from this trial displayed substantially less error. Modifications were made for the second trial in an attempt to produce viable results.

In the second trial, the water in the calorimeter rested longer at room temperature before the data was collected. This modification produced a result of 305.4 Joules per kilogram kelvin, which was 67.9% accurate to the theoretical value of grade 316 stainless steel, 470.

Another modification was used for the third and fourth trial to determine the change in accuracy when using a conductive calorimeter. A standard beverage thermos was used as the calorimeter for these trials. The thermometer used to measure temperature was upgraded to a digital one with long wire probes that enabled the thermos to have a tight seal. The first trial using this modification produced a result of 553.29 Joules per kilogram kelvin, which is 84.9% accurate, however, it was above the theoretical value. Accuracy above theoretical value indicated that an error was made.

Using a thermos as the calorimeter means that the water would take longer to reach room temperature . It is debatable if the water inside the thermos not being at room temperature would affect the results of the experiment. However, after further analysis the size of the thermos was determined as the cause of error in accuracy values. Due to the large size of the thermos, additional spaced remained inside the container for room temperature air to be trapped when the lid was placed on. This large volume of air was in direct contact with the water inside the thermos and affected the water’s temperature.

A further modification was made for the fourth trial of this experiment to limit error caused by the room temperature air. Only enough water to cover the sample was added and it was stressed that this water was at room temperature. This modification received results of 367.56 Joules per kilogram kelvin, which is 78.2% accurate.

4.0 Conclusion

An accurate result was not the goal of these experiments. Science is a slow process that is full of opportunity for mistakes, trial and error, and improvement. Scientific theories take years to develop and even longer for the scientific community to accept them. Science is an art and should be played with. Most earth-shattering discoveries were made by accident or with a different end goal in mind. For experiments such as the one described above, it is good practice to aim for an 80% accuracy for an at home value. When experimenting, it is key to have an open mind, roll with punches and most of all be safe.

5.0 References

‘Theory of Heat’ – Maxwell, James Clerk – page 57-67 – Westport, Conn., Greenwood Press – 1970: https://archive.org/details/theoryheat04maxwgoog/page/n77 -Talks about conservation of heat, the form, function and a bit of history of calorimeters, and the Method of Mixture. It is also a good book to understand heat in general, and it’s free.

Author: Cole Boucher, Junior Technical Writer at Thermtest

Can’t find the right product for your testing?