problem solving using trigonometric ratios

Problems on Trigonometric Ratios

Some trigonometric solutions based problems on trigonometric ratios are shown here with the step-by-step explanation.

1. If sin θ = 8/17, find other trigonometric ratios of <θ.

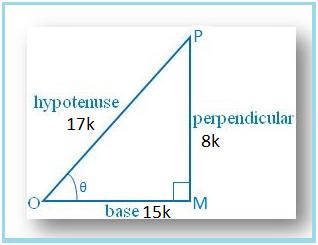
Let us draw a ∆ OMP in which ∠M = 90°.

Then sin θ = MP/OP = 8/17.

Let MP = 8k and OP = 17k, where k is positive.

By Pythagoras’ theorem, we get

Therefore, sin θ = MP/OP = 8k/17k = 8/17

cos θ = OM/OP = 15k/17k = 15/17

tan θ = Sin θ/Cos θ = (8/17 × 17/15) = 8/15

csc θ = 1/sin θ = 17/8

sec θ = 1/cos θ = 17/15 and

cot θ = 1/tan θ = 15/8.

2. If Cos A = 9/41, find other trigonometric ratios of ∠A.

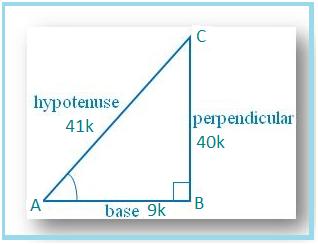
Let us draw a ∆ ABC in which ∠B = 90°.

Then cos θ = AB/AC = 9/41.

Let AB = 9k and AC = 41k, where k is positive.

Therefore, sin A = BC/AC = 40k/41k = 40/41

cos A = AB/AC = = 9k/41k = 9/41

tan A = Sin A/Cos A = (40/41 × 41/9) = 40/9

csc A = 1/sin A = 41/40

sec A = 1/cos A = 41/9 and

cot A = 1/tan A = 9/40.

3. Show that the value of sin θ and cos θ cannot be more than 1.

We know, in a right angle triangle the hypotenuse is the longest side.

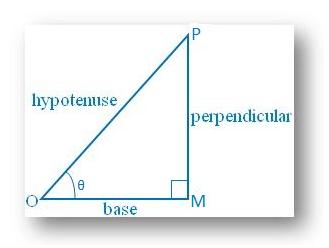
sin θ = perpendicular/hypotenuse = MP/OP < 1 since perpendicular cannot be greater than hypotenuse; sin θ cannot be more than 1.

Similarly, cos θ = base/hypotenuse = OM/OP < 1 since base cannot be greater than hypotenuse; cos θ cannot be more than 1.

4. Is that possible when A and B be acute angles, sin A = 0.3 and cos B = 0.7?

Since A and B are acute angles, 0 ≤ sin A ≤ 1 and 0 ≤ cos B ≤ 1, that means the value of sin A and cos B lies between 0 to 1. So, it is possible that sin A = 0.3 and cos B = 0.7

5. If 0° ≤ A ≤ 90° can sin A = 0.4 and cos A = 0.5 be possible?

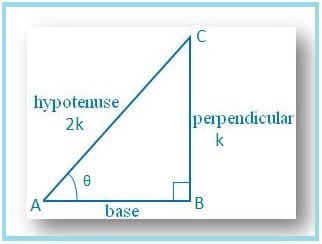
Let us draw a ∆ ABC in which ∠B = 90° and ∠BAC = θ.

Then sin θ = BC/AC = 1/2.

Let BC = k and AC = 2k, where k is positive.

= 3√3/2 - 4 × 3√3/8

= 3√3/2 - 3√3/2

Hence, (3cos θ - 4 cos³ θ) = 0.

7. Show that sin α + cos α > 1 when 0 ° ≤ α ≤ 90°

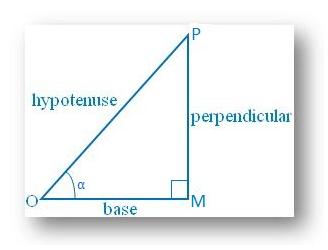
From the right triangle MOP,

Sin α = perpendicular/ hypotenuse

Cos α = base/ hypotenuse

Now, Sin α + Cos α

= perpendicular/ hypotenuse + base/ hypotenuse

= (perpendicular + base)/hypotenuse, which is > 1, Since we know that the sum of two sides of a triangle is always greater than the third side.

8. If cos θ = 3/5, find the value of (5csc θ - 4 tan θ)/(sec θ + cot θ)

Let ∠A = θ°

Then cos θ = AB/AC = 3/5.

Let AB = 3k and AC = 5k, where k is positive.

Therefore, sec θ = 1/cos θ = 5/3

tan θ = BC/AB =4k/3k = 4/3

cot θ = 1/tan θ = 3/4 and

csc θ = AC/BC = 5k/4k = 5/4

Now (5csc θ -4 tan θ)/(sec θ + cot θ)

= (5 × 5/4 - 4 × 4/3)/(5/3 + 3/4)

= (25/4 -16/3)/(5/3 +3/4)

= 11/12 × 12/29

9. Express 1 + 2 sin A cos A as a perfect square.

1 + 2 sin A cos A

10. If sin A + cos A = 7/5 and sin A cos A =12/25, find the values of sin A and cos A.

sin A + cos A = 7/5

⇒ cos A = 7/5 - sin θ

Now from sin θ/cos θ = 12/25

We get, sin θ(7/5 - sin θ) = 12/25

or, 5 sin θ(5 sin θ - 4) - 3(5 sin θ - 4) = 0

or, (5 sin θ - 3) (5 sin θ - 4) = 0

⇒ (5 sin θ - 3) = 0 or, (5 sin θ - 4) = 0

⇒ sin θ = 3/5 or, sin θ = 4/5

When sin θ = 3/5, cos θ = 12/25 × 5/3 = 4/5

Again, when sin θ = 4/5, cos θ = 12/25 × 5/4 = 3/5

Therefore, sin θ =3/5, cos θ = 4/5

or, sin θ =4/5, cos θ = 3/5.

11. If 3 tan θ = 4, evaluate (3sin θ + 2 cos θ)/(3sin θ - 2cos θ).

Solution: Given,

3 tan θ = 4

⇒ tan θ = 4/3

(3sin θ + 2 cos θ)/(3sin θ - 2cos θ)

= (3 tan θ + 2)/(3 tan θ - 2), [dividing both numerator and denominator by cos θ]

= (3 × 4/3 + 2)/(3 × 4/3 -2), putting the value of tan θ = 4/3

12. If (sec θ + tan θ)/(sec θ - tan θ) = 209/79, find the value of θ.

Solution: (sec θ + tan θ)/(sec θ - tan θ) = 209/79

⇒ [(sec θ + tan θ) - (sec θ - tan θ)]/[(sec θ + tan θ) + (sec θ - tan θ)] = [209 – 79]/[209 + 79], (Applying componendo and dividendo)

⇒ 2 tan θ/2 sec θ =130/288

⇒ sin θ/cos θ × cos θ = 65/144

⇒ sin θ = 65/144.

13. If 5 cot θ = 3, find the value of (5 sin θ - 3 cos θ)/(4 sin θ + 3 cos θ).

Given 5 cot θ = 3

⇒ cot θ = 3/5

Now (5 sin θ - 3 cos θ)/(4 sin θ + 3 cos θ)

= (5 - 3 cot θ)/(4 sin θ + 3 cot θ), [dividing both numerator and denominator by sin θ]

= (5 - 3 × 3/5)/(4 + 3 × 3/5)

= (5 - 9/5)/(4 + 9/5)

= (16/5 × 5/29)

⇒ sin θ(sin θ - 2) - 1(sin θ - 2) = 0

⇒ (sin θ - 2)(sin θ - 1) = 0

⇒ (sin θ - 2) = 0 or, (sin θ - 1) = 0

⇒ sin θ = 2 or, sin θ = 1

So, value of sin θ can’t be greater than 1,

Therefore sin θ = 1

Basic Trigonometric Ratios  

Relations Between the Trigonometric Ratios

Reciprocal Relations of Trigonometric Ratios

Trigonometrical Identity

Problems on Trigonometric Identities

Elimination of Trigonometric Ratios  

Eliminate Theta between the equations

Problems on Eliminate Theta  

Trig Ratio Problems

Proving Trigonometric Ratios

Trig Ratios Proving Problems

Verify Trigonometric Identities  

• 10th Grade Math

From Problems on Trigonometric Ratios to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

Share this page: What’s this?

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

2nd grade math Worksheets | Free Math Worksheets | By Grade and Topic

Nov 20, 24 01:00 PM

2nd Grade Measurement Worksheet | Measuring Length, Mass and Volume

Nov 20, 24 12:50 AM

2nd Grade Fractions Worksheet | Basic Concept of Fractions | Answers

Nov 20, 24 12:16 AM

2nd Grade Math Practice | Second Grade Math |2nd Grade Math Worksheets

Nov 18, 24 02:23 PM

Worksheet on Addition of Length | Word Problems on Addition of Length

Nov 17, 24 10:29 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Trigonometric Ratios

A series of free, online High School Geometry Video Lessons and solutions. In these lessons, we will learn

• how to find the sine of an angle in a right triangle,
• how to find the cosine of an angle in a right triangle,
• how to find the tangent of an angle in a right triangle,
• how to use inverse trigonometric functions to find an angle with a given trigonometric value.

Related Pages Using SOH-CAH-TOA Trigonometry Word Problems Inverse trigonometry Lessons On Trigonometry Trigonometry Worksheets

The following diagram shows the trigonometric ratios using SOHCAHTOA. Scroll down the page if you need more examples and solutions on how to use the trigonometric ratios.

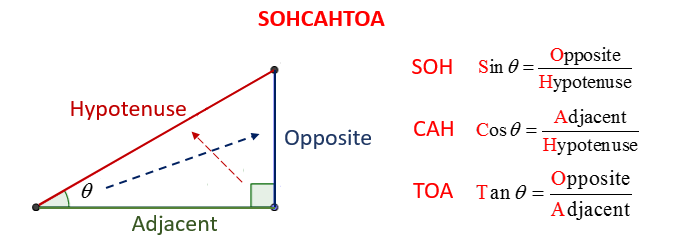
Trigonometric Ratios: Sine

Right triangles have ratios to represent the angles formed by the hypotenuse and its legs. Sine ratios, along with cosine and tangent ratios, are ratios of the lengths of two sides of the triangle. Sine ratios in particular are the ratios of the length of the side opposite the angle they represent over the hypotenuse. Sine ratios are useful in trigonometry when dealing with triangles and circles.

How to define the sine ratio and identify the sine of an angle in a right triangle?

Identify the hypotenuse of a right triangle. sin θ = opposite/hypotenuse

A word problem involving the trigonometric ratio of sine to calculate the height of a pole

Example: A 55 ft wire connects a point on the ground to the top of a pole. The cable makes an angle of 60° with the ground. Find the height of the pole to the nearest foot.

Trigonometric Ratios: Cosine

Right triangles have ratios that are used to represent their base angles. Cosine ratios, along with sine and tangent ratios, are ratios of two different sides of a right triangle.Cosine ratios are specifically the ratio of the side adjacent to the represented base angle over the hypotenuse. In order to find the measure of the angle, we must understand inverse trigonometric functions.

How to use the Cosine formula (the CAH Formula) to find missing sides or angles?

Cosine θ = adjacent/hypotenuse

Example: Find the missing side or angle a) cos 30° = x/2 b) cos 37° = 4.2/x c) cos θ = 63/80

How to apply the Sine and Cosine Ratios?

Sine, cosine are trigonometric ratios for the acute angles and involve the length of a leg and the hypotenuse of a right triangle.

Angle of elevation - When looking up at an object, the angle your line of sight makes with a horizontal line is called the angle of elevation.

Angle of depression - When looking down at an object, the angle your line of sight makes with a horizontal line is called the angle of depression.

• Find sin U and sin W. Write each answer as a fraction and as a decimal rounded to four places.
• Find cos S and cos R. Write each answer as a fraction and as a decimal rounded to four places.
• You walk from one corner of a basketball court to the opposite corner. write and solve a proportion using a trigonometric ratio to approximate the distance of the walk.
• You are at the top of a roller coaster 100 feet above the ground. The angle of depression is 44°. About how far do you ride down the hill?
• A railroad crossing arm that is 20 feet long is stuck with an angle of elevation of 35°. Find the lengths of x and y.
• Use a special right triangle to find the sine and cosine of a 30° angle.

Trigonometric Ratios: Tangent

Right triangles have ratios that are used to represent their base angles. Tangent ratios, along with cosine and sine ratios, are ratios of two different sides of a right triangle. Tangent ratios are the ratio of the side opposite to the side adjacent the angle they represent. In order to find the measure of the angle itself, one must understand inverse trigonometric functions.

How to use the Tangent formula (the TOA Formula)?

Tangent θ = opposite/adjacent

Example: Find the missing side or angle a) tan 28° = x/40 b) tan 41° = 1.9/x c) tan θ = 11/8

Applications of Trigonometric Ratios (Word Problems Involving Tangent, Sine and Cosine)

• Find the area of the parallelogram.
• A 70 foot ramp rises from the first floor to the second floor of a parking garage. The ramp makes an angle with the ground. How high above the first floor is the second floor?
• You see Mr. Wandera flying a kite in the park. The kite string is 65 meters long. What angle does the string need to form with the ground so that the kite is 30 feet off of the ground?
• From the top of a 100-foot lookout tower, a forest ranger spotted a fire at a 25° angle of depression. How far was the fire from the base of the lookout tower?
• An 8 foot ladder is leaning against a wall. The ladder makes a 53° angle with the wall. How high does the ladder reach?

Inverse Trigonometric Functions

Once we understand the trigonometric functions sine, cosine, and tangent, we are ready to learn how to use inverse trigonometric functions to find the measure of the angle the function represents. Inverse trigonometric functions, found on any standard scientific or graphing calculator, are a vital part of trigonometry and will be encountered often in Calculus.

How to use inverse trigonometric functions to find an angle with a given trigonometric value and how to use inverse trigonometric functions to solve a right triangle?

Example: Use the calculator to find an angle θ in the interval [0, 90] that satisfies the equation.

• sin θ = 0.7523
• tan θ = 3.54
• Solve the given right triangle if a = 44.3 cm and b = 55.9 cm.
• Find each angle in a 3,4,5 triangle

How to use inverse trig to find a missing angle?

Inverse trig functions are used to find missing angles rather than missing sides.

Find missing Angles - Using Inverse Sine, Cosine, Tangent

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

PROBLEMS ON TRIGONOMETRIC RATIOS

Problem 1 :

For the measures in the figure shown below, compute sine, cosine and tangent ratios of the angle θ.

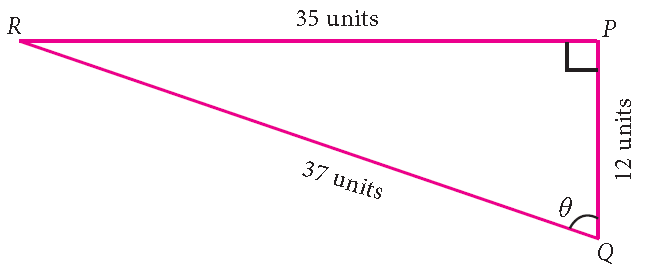
In the given right angled triangle, note that for the given angle θ, PR is the ‘opposite’ side and PQ is the ‘adjacent’ side.

Then, 

sin θ  =  opposite side/hypotenuse  =  PR/QR  =  35/37

cos θ  =  adjacent side/hypotenuse = PQ/QR  =  12/37

tan θ  =  opposite side / adjacent side  =  PR/PQ  =  35/12

Problem 2 :

Find the six trigonometric ratios of the angle θ using the diagram shown below. 

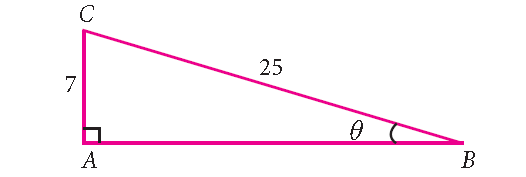
In the given right angled triangle, note that for the given angle θ, AC is the ‘opposite’ side and AB is the ‘adjacent’ side.

And also, the length of the adjacent side 'AB' is not given. 

Find the length of AB.

By Pythagorean Theorem,

BC 2   =  AB 2  + AC 2

25 2   =  AB 2  + 7 2

625  =  AB 2 + 49

Subtract 49 from each side. 

576  =  AB 2

24 2   =  AB 2

24  =  AB  

sin θ  =  opposite side/hypotenuse  =   AC/ BC  =  7/25

cos θ  =  adjacent side/hypotenuse  =  AB/BC  =  24/25

tan θ  =  opposite side/adjacent side  =  AC/AB  =  7/24

csc θ  =  1/s in θ  =  25/7

sec θ  =  1/cos θ  =   25/24

cot θ  =  1/tan θ  =   24/7

Problem 3 :

If tanA = 2/3, then find all the other trigonometric ratios. 

tanA  =  opposite side/adjacent side  =  2/3

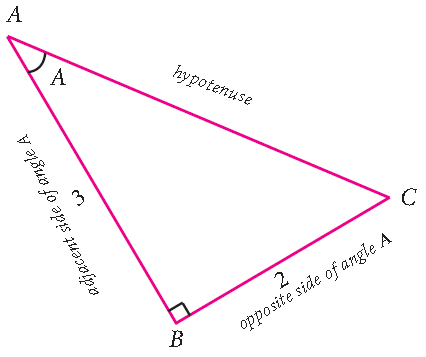
AC 2   =  AB 2  + BC 2

AC 2   =  3 2  + 2 2

AC 2   =  9 + 4

AC 2   =  13

AC  =  √13

sinA   =  opposite side/hypotenuse  =   BC/ AC  =  2/ √ 13

cosA   =  adjacent side/hypotenuse  =  AB/AC  =  3/ √13

cscA   =  1/s inA   =   √13 /2

secA   =  1/cosA   =   √13 /3

cotA   =  1/tanA   =  3/2

Problem 4 :

If sec θ   =  2/3, then find the value of

(2sinθ - 3cosθ)/(4sinθ - 9cosθ)  

sec θ   =  hypotenuse/adjacent side  =  13/5

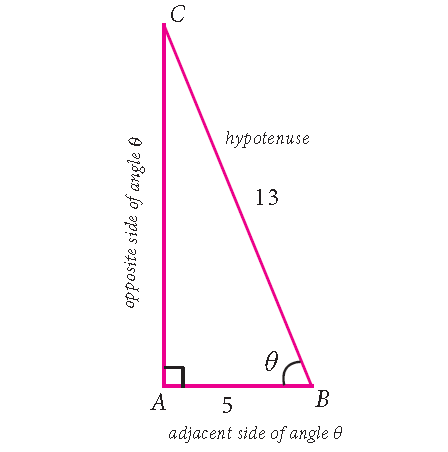
13 2   =  5 2  + AC 2

169  =  25 + AC 2

Subtract 25 from each side. 

144  =  AC 2

12 2   =  AC 2

12  =   AC

sin θ   =  opposite side/hypotenuse  =   AC/BC  =  12/1 3

cos θ    =  adjacent side/hypotenuse  =  AB/BC  =  5/ 13

(2sinθ - 3cosθ)/(4sinθ - 9cosθ) : 

=  (2  ⋅  12/13 - 3  ⋅  5/13)/(4  ⋅ 12/13 - 9  ⋅ 5/13)

=  (24 /13 - 1 5/13)/(48 /13 - 45/13)

=  [(24 - 15)/13]/[(48 - 45)/13]

=  (9/13)/(3/13)

=  (9/13)  ⋅  (13/3)

=  9/3

(2sinθ - 3cosθ)/(4sinθ - 9cosθ)   =  3

To learn SOHCAHTOA in detail,

please click here

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

SAT Math Resources (Videos, Concepts, Worksheets and More)

Nov 21, 24 06:23 AM

Digital SAT Math Problems and Solutions (Part - 75)

Nov 21, 24 06:13 AM

Digital SAT Math Problems and Solutions (Part - 74)

Nov 20, 24 08:12 AM