young's experiment light waves

27.3 Young’s Double Slit Experiment

Learning objectives.

By the end of this section, you will be able to:

• Explain the phenomena of interference.
• Define constructive interference for a double slit and destructive interference for a double slit.

Although Christiaan Huygens thought that light was a wave, Isaac Newton did not. Newton felt that there were other explanations for color, and for the interference and diffraction effects that were observable at the time. Owing to Newton’s tremendous stature, his view generally prevailed. The fact that Huygens’s principle worked was not considered evidence that was direct enough to prove that light is a wave. The acceptance of the wave character of light came many years later when, in 1801, the English physicist and physician Thomas Young (1773–1829) did his now-classic double slit experiment (see Figure 27.10 ).

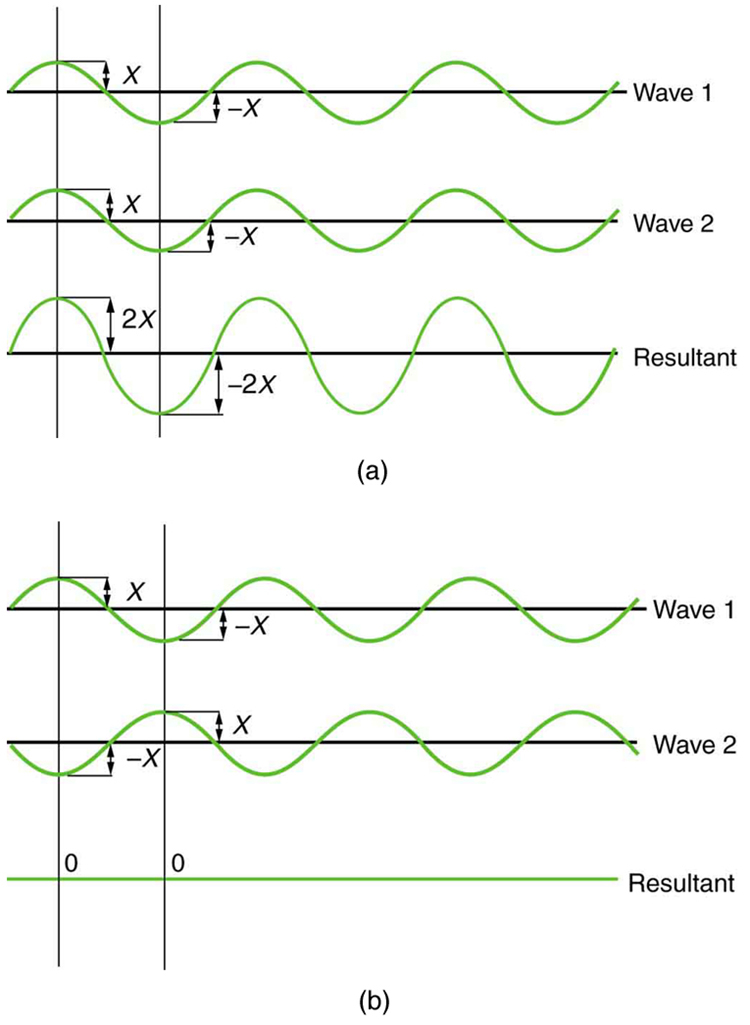
Why do we not ordinarily observe wave behavior for light, such as observed in Young’s double slit experiment? First, light must interact with something small, such as the closely spaced slits used by Young, to show pronounced wave effects. Furthermore, Young first passed light from a single source (the Sun) through a single slit to make the light somewhat coherent. By coherent , we mean waves are in phase or have a definite phase relationship. Incoherent means the waves have random phase relationships. Why did Young then pass the light through a double slit? The answer to this question is that two slits provide two coherent light sources that then interfere constructively or destructively. Young used sunlight, where each wavelength forms its own pattern, making the effect more difficult to see. We illustrate the double slit experiment with monochromatic (single λ λ ) light to clarify the effect. Figure 27.11 shows the pure constructive and destructive interference of two waves having the same wavelength and amplitude.

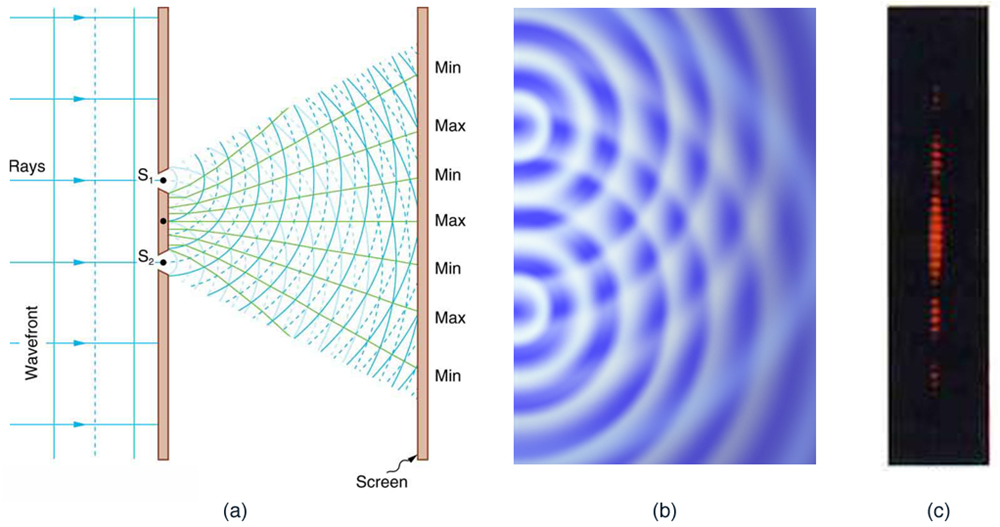
When light passes through narrow slits, it is diffracted into semicircular waves, as shown in Figure 27.12 (a). Pure constructive interference occurs where the waves are crest to crest or trough to trough. Pure destructive interference occurs where they are crest to trough. The light must fall on a screen and be scattered into our eyes for us to see the pattern. An analogous pattern for water waves is shown in Figure 27.12 (b). Note that regions of constructive and destructive interference move out from the slits at well-defined angles to the original beam. These angles depend on wavelength and the distance between the slits, as we shall see below.

To understand the double slit interference pattern, we consider how two waves travel from the slits to the screen, as illustrated in Figure 27.13 . Each slit is a different distance from a given point on the screen. Thus different numbers of wavelengths fit into each path. Waves start out from the slits in phase (crest to crest), but they may end up out of phase (crest to trough) at the screen if the paths differ in length by half a wavelength, interfering destructively as shown in Figure 27.13 (a). If the paths differ by a whole wavelength, then the waves arrive in phase (crest to crest) at the screen, interfering constructively as shown in Figure 27.13 (b). More generally, if the paths taken by the two waves differ by any half-integral number of wavelengths [ ( 1 / 2 ) λ ( 1 / 2 ) λ , ( 3 / 2 ) λ ( 3 / 2 ) λ , ( 5 / 2 ) λ ( 5 / 2 ) λ , etc.], then destructive interference occurs. Similarly, if the paths taken by the two waves differ by any integral number of wavelengths ( λ λ , 2 λ 2 λ , 3 λ 3 λ , etc.), then constructive interference occurs.

Take-Home Experiment: Using Fingers as Slits

Look at a light, such as a street lamp or incandescent bulb, through the narrow gap between two fingers held close together. What type of pattern do you see? How does it change when you allow the fingers to move a little farther apart? Is it more distinct for a monochromatic source, such as the yellow light from a sodium vapor lamp, than for an incandescent bulb?

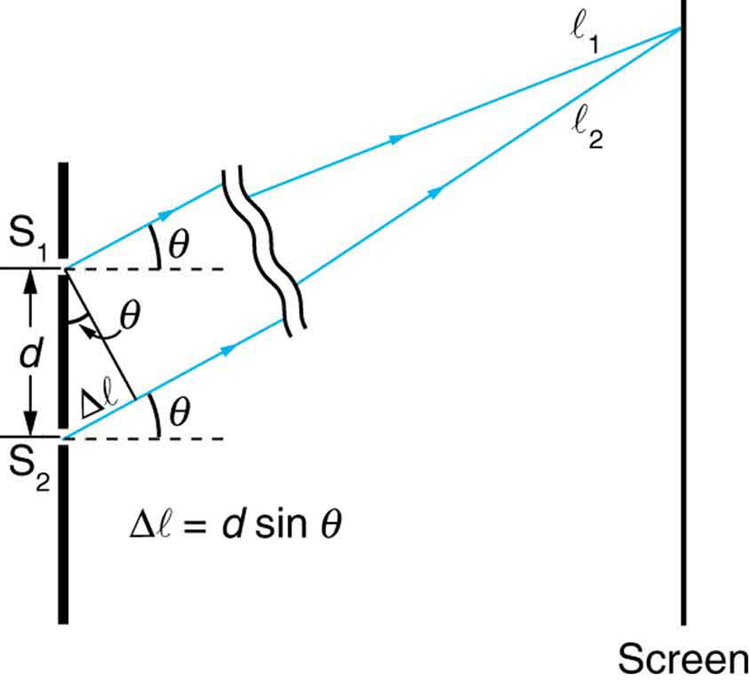
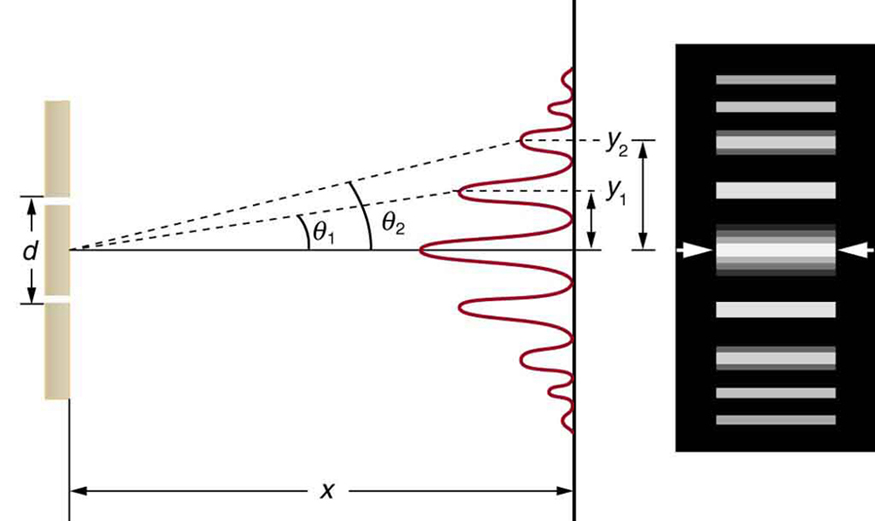
Figure 27.14 shows how to determine the path length difference for waves traveling from two slits to a common point on a screen. If the screen is a large distance away compared with the distance between the slits, then the angle θ θ between the path and a line from the slits to the screen (see the figure) is nearly the same for each path. The difference between the paths is shown in the figure; simple trigonometry shows it to be d sin θ d sin θ , where d d is the distance between the slits. To obtain constructive interference for a double slit , the path length difference must be an integral multiple of the wavelength, or

Similarly, to obtain destructive interference for a double slit , the path length difference must be a half-integral multiple of the wavelength, or

where λ λ is the wavelength of the light, d d is the distance between slits, and θ θ is the angle from the original direction of the beam as discussed above. We call m m the order of the interference. For example, m = 4 m = 4 is fourth-order interference.

The equations for double slit interference imply that a series of bright and dark lines are formed. For vertical slits, the light spreads out horizontally on either side of the incident beam into a pattern called interference fringes, illustrated in Figure 27.15 . The intensity of the bright fringes falls off on either side, being brightest at the center. The closer the slits are, the more is the spreading of the bright fringes. We can see this by examining the equation

For fixed λ λ and m m , the smaller d d is, the larger θ θ must be, since sin θ = mλ / d sin θ = mλ / d . This is consistent with our contention that wave effects are most noticeable when the object the wave encounters (here, slits a distance d d apart) is small. Small d d gives large θ θ , hence a large effect.

Example 27.1

Finding a wavelength from an interference pattern.

Suppose you pass light from a He-Ne laser through two slits separated by 0.0100 mm and find that the third bright line on a screen is formed at an angle of 10 . 95º 10 . 95º relative to the incident beam. What is the wavelength of the light?

The third bright line is due to third-order constructive interference, which means that m = 3 m = 3 . We are given d = 0 . 0100 mm d = 0 . 0100 mm and θ = 10 . 95º θ = 10 . 95º . The wavelength can thus be found using the equation d sin θ = mλ d sin θ = mλ for constructive interference.

The equation is d sin θ = mλ d sin θ = mλ . Solving for the wavelength λ λ gives

Substituting known values yields

To three digits, this is the wavelength of light emitted by the common He-Ne laser. Not by coincidence, this red color is similar to that emitted by neon lights. More important, however, is the fact that interference patterns can be used to measure wavelength. Young did this for visible wavelengths. This analytical technique is still widely used to measure electromagnetic spectra. For a given order, the angle for constructive interference increases with λ λ , so that spectra (measurements of intensity versus wavelength) can be obtained.

Example 27.2

Calculating highest order possible.

Interference patterns do not have an infinite number of lines, since there is a limit to how big m m can be. What is the highest-order constructive interference possible with the system described in the preceding example?

Strategy and Concept

The equation d sin θ = mλ (for m = 0, 1, − 1, 2, − 2, … ) d sin θ = mλ (for m = 0, 1, − 1, 2, − 2, … ) describes constructive interference. For fixed values of d d and λ λ , the larger m m is, the larger sin θ sin θ is. However, the maximum value that sin θ sin θ can have is 1, for an angle of 90º 90º . (Larger angles imply that light goes backward and does not reach the screen at all.) Let us find which m m corresponds to this maximum diffraction angle.

Solving the equation d sin θ = mλ d sin θ = mλ  for  m m gives

Taking sin θ = 1 sin θ = 1 and substituting the values of d d and λ λ from the preceding example gives

Therefore, the largest integer m m can be is 15, or

The number of fringes depends on the wavelength and slit separation. The number of fringes will be very large for large slit separations. However, if the slit separation becomes much greater than the wavelength, the intensity of the interference pattern changes so that the screen has two bright lines cast by the slits, as expected when light behaves like a ray. We also note that the fringes get fainter further away from the center. Consequently, not all 15 fringes may be observable.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: College Physics 2e
• Publication date: Jul 13, 2022
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
• Section URL: https://openstax.org/books/college-physics-2e/pages/27-3-youngs-double-slit-experiment

© Jul 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Wave Optics

Young’s double slit experiment, learning objectives.

By the end of this section, you will be able to:

• Explain the phenomena of interference.
• Define constructive interference for a double slit and destructive interference for a double slit.

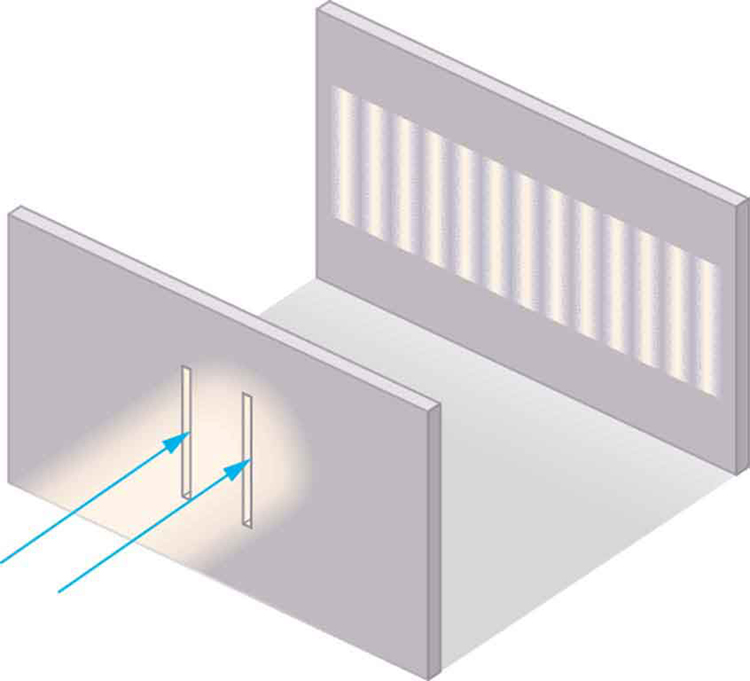
Although Christiaan Huygens thought that light was a wave, Isaac Newton did not. Newton felt that there were other explanations for color, and for the interference and diffraction effects that were observable at the time. Owing to Newton’s tremendous stature, his view generally prevailed. The fact that Huygens’s principle worked was not considered evidence that was direct enough to prove that light is a wave. The acceptance of the wave character of light came many years later when, in 1801, the English physicist and physician Thomas Young (1773–1829) did his now-classic double slit experiment (see Figure 1).

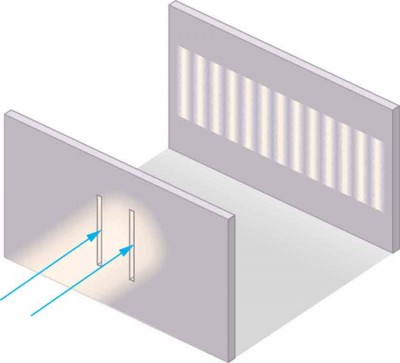
Figure 1. Young’s double slit experiment. Here pure-wavelength light sent through a pair of vertical slits is diffracted into a pattern on the screen of numerous vertical lines spread out horizontally. Without diffraction and interference, the light would simply make two lines on the screen.

Why do we not ordinarily observe wave behavior for light, such as observed in Young’s double slit experiment? First, light must interact with something small, such as the closely spaced slits used by Young, to show pronounced wave effects. Furthermore, Young first passed light from a single source (the Sun) through a single slit to make the light somewhat coherent. By coherent , we mean waves are in phase or have a definite phase relationship. Incoherent means the waves have random phase relationships. Why did Young then pass the light through a double slit? The answer to this question is that two slits provide two coherent light sources that then interfere constructively or destructively. Young used sunlight, where each wavelength forms its own pattern, making the effect more difficult to see. We illustrate the double slit experiment with monochromatic (single λ ) light to clarify the effect. Figure 2 shows the pure constructive and destructive interference of two waves having the same wavelength and amplitude.

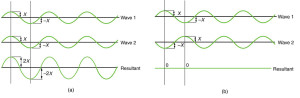
Figure 2. The amplitudes of waves add. (a) Pure constructive interference is obtained when identical waves are in phase. (b) Pure destructive interference occurs when identical waves are exactly out of phase, or shifted by half a wavelength.

When light passes through narrow slits, it is diffracted into semicircular waves, as shown in Figure 3a. Pure constructive interference occurs where the waves are crest to crest or trough to trough. Pure destructive interference occurs where they are crest to trough. The light must fall on a screen and be scattered into our eyes for us to see the pattern. An analogous pattern for water waves is shown in Figure 3b. Note that regions of constructive and destructive interference move out from the slits at well-defined angles to the original beam. These angles depend on wavelength and the distance between the slits, as we shall see below.

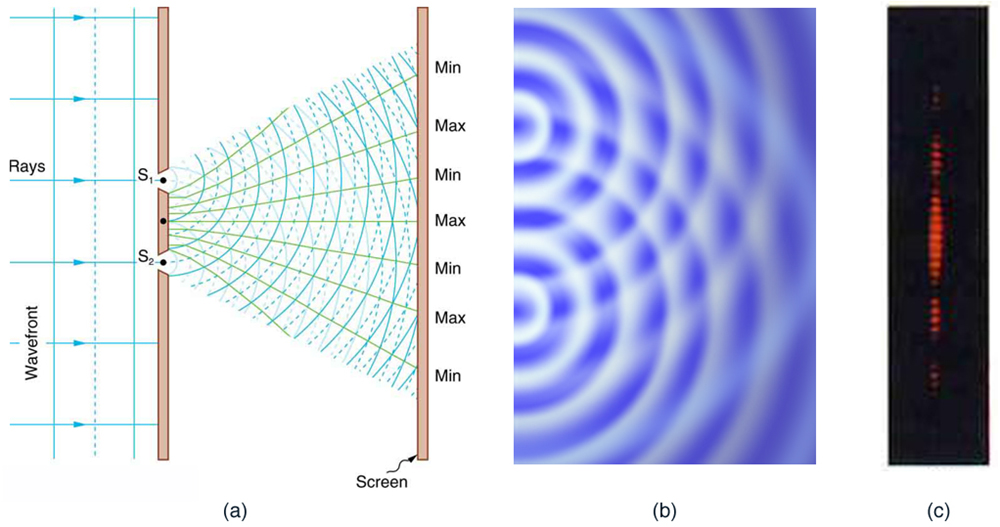
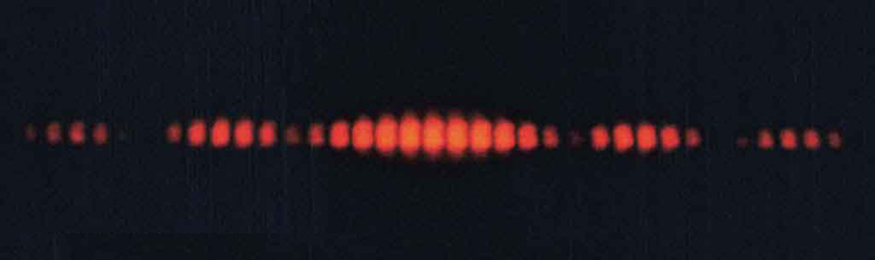
Figure 3. Double slits produce two coherent sources of waves that interfere. (a) Light spreads out (diffracts) from each slit, because the slits are narrow. These waves overlap and interfere constructively (bright lines) and destructively (dark regions). We can only see this if the light falls onto a screen and is scattered into our eyes. (b) Double slit interference pattern for water waves are nearly identical to that for light. Wave action is greatest in regions of constructive interference and least in regions of destructive interference. (c) When light that has passed through double slits falls on a screen, we see a pattern such as this. (credit: PASCO)

To understand the double slit interference pattern, we consider how two waves travel from the slits to the screen, as illustrated in Figure 4. Each slit is a different distance from a given point on the screen. Thus different numbers of wavelengths fit into each path. Waves start out from the slits in phase (crest to crest), but they may end up out of phase (crest to trough) at the screen if the paths differ in length by half a wavelength, interfering destructively as shown in Figure 4a. If the paths differ by a whole wavelength, then the waves arrive in phase (crest to crest) at the screen, interfering constructively as shown in Figure 4b. More generally, if the paths taken by the two waves differ by any half-integral number of wavelengths [(1/2) λ , (3/2) λ , (5/2) λ , etc.], then destructive interference occurs. Similarly, if the paths taken by the two waves differ by any integral number of wavelengths ( λ , 2 λ , 3 λ , etc.), then constructive interference occurs.

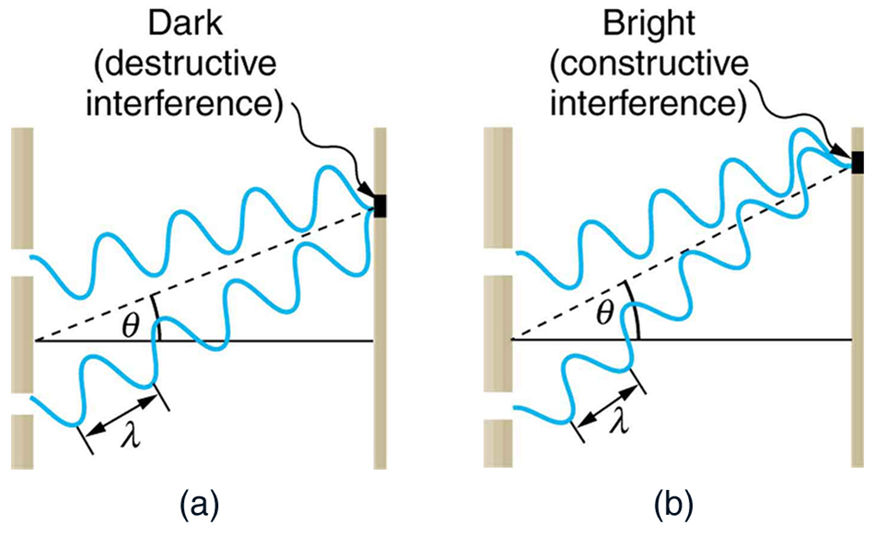
Figure 4. Waves follow different paths from the slits to a common point on a screen. (a) Destructive interference occurs here, because one path is a half wavelength longer than the other. The waves start in phase but arrive out of phase. (b) Constructive interference occurs here because one path is a whole wavelength longer than the other. The waves start out and arrive in phase.

Take-Home Experiment: Using Fingers as Slits

Look at a light, such as a street lamp or incandescent bulb, through the narrow gap between two fingers held close together. What type of pattern do you see? How does it change when you allow the fingers to move a little farther apart? Is it more distinct for a monochromatic source, such as the yellow light from a sodium vapor lamp, than for an incandescent bulb?

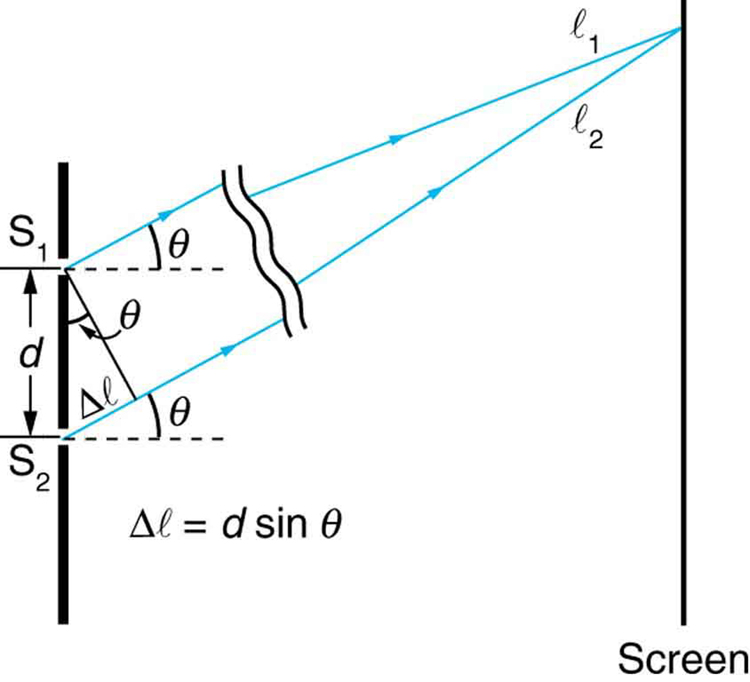
Figure 5. The paths from each slit to a common point on the screen differ by an amount dsinθ, assuming the distance to the screen is much greater than the distance between slits (not to scale here).

Figure 5 shows how to determine the path length difference for waves traveling from two slits to a common point on a screen. If the screen is a large distance away compared with the distance between the slits, then the angle θ between the path and a line from the slits to the screen (see the figure) is nearly the same for each path. The difference between the paths is shown in the figure; simple trigonometry shows it to be d sin  θ , where d is the distance between the slits. To obtain constructive interference for a double slit , the path length difference must be an integral multiple of the wavelength, or  d sin  θ = mλ, for   m = 0, 1, −1, 2, −2, . . . (constructive).

Similarly, to obtain destructive interference for a double slit , the path length difference must be a half-integral multiple of the wavelength, or

[latex]d\sin\theta=\left(m+\frac{1}{2}\right)\lambda\text{, for }m=0,1,-1,2,-2,\dots\text{ (destructive)}\\[/latex],

where λ is the wavelength of the light, d is the distance between slits, and θ is the angle from the original direction of the beam as discussed above. We call m the order of the interference. For example, m  = 4 is fourth-order interference.

The equations for double slit interference imply that a series of bright and dark lines are formed. For vertical slits, the light spreads out horizontally on either side of the incident beam into a pattern called interference fringes, illustrated in Figure 6. The intensity of the bright fringes falls off on either side, being brightest at the center. The closer the slits are, the more is the spreading of the bright fringes. We can see this by examining the equation  d sin  θ = mλ, for   m = 0, 1, −1, 2, −2, . . . .

For fixed λ and m , the smaller d is, the larger θ must be, since [latex]\sin\theta=\frac{m\lambda}{d}\\[/latex]. This is consistent with our contention that wave effects are most noticeable when the object the wave encounters (here, slits a distance d apart) is small. Small d gives large θ , hence a large effect.

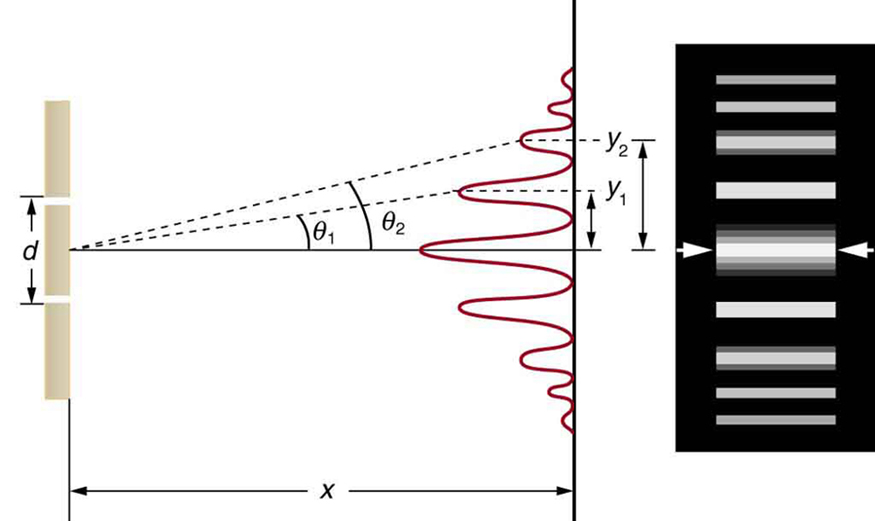
Figure 6. The interference pattern for a double slit has an intensity that falls off with angle. The photograph shows multiple bright and dark lines, or fringes, formed by light passing through a double slit.

Example 1. Finding a Wavelength from an Interference Pattern

Suppose you pass light from a He-Ne laser through two slits separated by 0.0100 mm and find that the third bright line on a screen is formed at an angle of 10.95º relative to the incident beam. What is the wavelength of the light?

The third bright line is due to third-order constructive interference, which means that m  = 3. We are given d = 0.0100 mm and θ  = 10.95º. The wavelength can thus be found using the equation  d sin  θ = mλ  for constructive interference.

The equation is d sin  θ = mλ . Solving for the wavelength λ gives [latex]\lambda=\frac{d\sin\theta}{m}\\[/latex].

Substituting known values yields

[latex]\begin{array}{lll}\lambda&=&\frac{\left(0.0100\text{ nm}\right)\left(\sin10.95^{\circ}\right)}{3}\\\text{ }&=&6.33\times10^{-4}\text{ nm}=633\text{ nm}\end{array}\\[/latex]

To three digits, this is the wavelength of light emitted by the common He-Ne laser. Not by coincidence, this red color is similar to that emitted by neon lights. More important, however, is the fact that interference patterns can be used to measure wavelength. Young did this for visible wavelengths. This analytical technique is still widely used to measure electromagnetic spectra. For a given order, the angle for constructive interference increases with λ , so that spectra (measurements of intensity versus wavelength) can be obtained.

Example 2. Calculating Highest Order Possible

Interference patterns do not have an infinite number of lines, since there is a limit to how big m can be. What is the highest-order constructive interference possible with the system described in the preceding example?

Strategy and Concept

The equation  d sin  θ = mλ ( for   m = 0, 1, −1, 2, −2, . . . ) describes constructive interference. For fixed values of d and λ , the larger m is, the larger sin  θ  is. However, the maximum value that sin  θ  can have is 1, for an angle of 90º. (Larger angles imply that light goes backward and does not reach the screen at all.) Let us find which m corresponds to this maximum diffraction angle.

Solving the equation  d sin  θ = mλ  for m gives [latex]\lambda=\frac{d\sin\theta}{m}\\[/latex].

Taking sin  θ = 1 and substituting the values of d and λ from the preceding example gives

[latex]\displaystyle{m}=\frac{\left(0.0100\text{ mm}\right)\left(1\right)}{633\text{ nm}}\approx15.8\\[/latex]

Therefore, the largest integer m can be is 15, or  m  = 15.

The number of fringes depends on the wavelength and slit separation. The number of fringes will be very large for large slit separations. However, if the slit separation becomes much greater than the wavelength, the intensity of the interference pattern changes so that the screen has two bright lines cast by the slits, as expected when light behaves like a ray. We also note that the fringes get fainter further away from the center. Consequently, not all 15 fringes may be observable.

Section Summary

• Young’s double slit experiment gave definitive proof of the wave character of light.
• An interference pattern is obtained by the superposition of light from two slits.
• There is constructive interference when  d sin  θ = mλ ( for   m = 0, 1, −1, 2, −2, . . . ), where d  is the distance between the slits, θ is the angle relative to the incident direction, and m  is the order of the interference.
• There is destructive interference when  d sin  θ = mλ ( for   m = 0, 1, −1, 2, −2, . . . ).

Conceptual Questions

• Young’s double slit experiment breaks a single light beam into two sources. Would the same pattern be obtained for two independent sources of light, such as the headlights of a distant car? Explain.
• Suppose you use the same double slit to perform Young’s double slit experiment in air and then repeat the experiment in water. Do the angles to the same parts of the interference pattern get larger or smaller? Does the color of the light change? Explain.
• Is it possible to create a situation in which there is only destructive interference? Explain.
• Figure 7 shows the central part of the interference pattern for a pure wavelength of red light projected onto a double slit. The pattern is actually a combination of single slit and double slit interference. Note that the bright spots are evenly spaced. Is this a double slit or single slit characteristic? Note that some of the bright spots are dim on either side of the center. Is this a single slit or double slit characteristic? Which is smaller, the slit width or the separation between slits? Explain your responses.

Figure 7. This double slit interference pattern also shows signs of single slit interference. (credit: PASCO)

Problems & Exercises

• At what angle is the first-order maximum for 450-nm wavelength blue light falling on double slits separated by 0.0500 mm?
• Calculate the angle for the third-order maximum of 580-nm wavelength yellow light falling on double slits separated by 0.100 mm.
• What is the separation between two slits for which 610-nm orange light has its first maximum at an angle of 30.0º?
• Find the distance between two slits that produces the first minimum for 410-nm violet light at an angle of 45.0º.
• Calculate the wavelength of light that has its third minimum at an angle of 30.0º when falling on double slits separated by 3.00 μm.
• What is the wavelength of light falling on double slits separated by 2.00 μm if the third-order maximum is at an angle of 60.0º?
• At what angle is the fourth-order maximum for the situation in Question 1?
• What is the highest-order maximum for 400-nm light falling on double slits separated by 25.0 μm?
• Find the largest wavelength of light falling on double slits separated by 1.20 μm for which there is a first-order maximum. Is this in the visible part of the spectrum?
• What is the smallest separation between two slits that will produce a second-order maximum for 720-nm red light?
• (a) What is the smallest separation between two slits that will produce a second-order maximum for any visible light? (b) For all visible light?
• (a) If the first-order maximum for pure-wavelength light falling on a double slit is at an angle of 10.0º, at what angle is the second-order maximum? (b) What is the angle of the first minimum? (c) What is the highest-order maximum possible here?

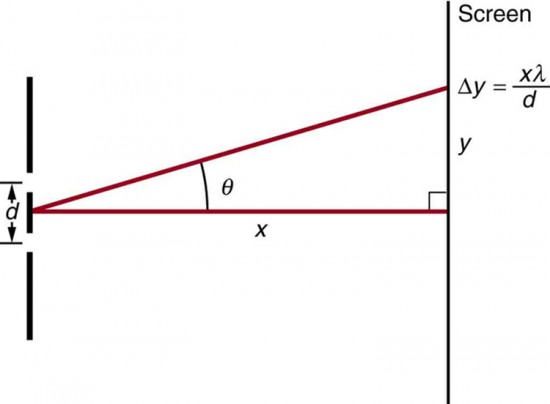
Figure 8. The distance between adjacent fringes is [latex]\Delta{y}=\frac{x\lambda}{d}\\[/latex], assuming the slit separation d  is large compared with λ .

• Using the result of the problem above, calculate the distance between fringes for 633-nm light falling on double slits separated by 0.0800 mm, located 3.00 m from a screen as in Figure 8.
• Using the result of the problem two problems prior, find the wavelength of light that produces fringes 7.50 mm apart on a screen 2.00 m from double slits separated by 0.120 mm (see Figure 8).

coherent:  waves are in phase or have a definite phase relationship

constructive interference for a double slit:  the path length difference must be an integral multiple of the wavelength

destructive interference for a double slit:  the path length difference must be a half-integral multiple of the wavelength

incoherent:  waves have random phase relationships

order:  the integer m  used in the equations for constructive and destructive interference for a double slit

Selected Solutions to Problems & Exercises

3. 1.22 × 10 −6 m

9. 1200 nm (not visible)

11. (a) 760 nm; (b) 1520 nm

13. For small angles sin θ − tan θ  ≈ θ  (in radians).

For two adjacent fringes we have,  d  sin θ m = mλ  and  d sin θ m + 1 = ( m  + 1) λ

Subtracting these equations gives

[latex]\begin{array}{}d\left(\sin{\theta }_{\text{m}+1}-\sin{\theta }_{\text{m}}\right)=\left[\left(m+1\right)-m\right]\lambda \\ d\left({\theta }_{\text{m}+1}-{\theta }_{\text{m}}\right)=\lambda \\ \text{tan}{\theta }_{\text{m}}=\frac{{y}_{\text{m}}}{x}\approx {\theta }_{\text{m}}\Rightarrow d\left(\frac{{y}_{\text{m}+1}}{x}-\frac{{y}_{\text{m}}}{x}\right)=\lambda \\ d\frac{\Delta y}{x}=\lambda \Rightarrow \Delta y=\frac{\mathrm{x\lambda }}{d}\end{array}\\[/latex]

Candela Citations

• College Physics. Authored by : OpenStax College. Located at : http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a/College_Physics . License : CC BY: Attribution . License Terms : Located at License

Chapter 27 Wave Optics

27.3 Young’s Double Slit Experiment

• Explain the phenomena of interference.
• Define constructive interference for a double slit and destructive interference for a double slit.

Although Christiaan Huygens thought that light was a wave, Isaac Newton did not. Newton felt that there were other explanations for color, and for the interference and diffraction effects that were observable at the time. Owing to Newton’s tremendous stature, his view generally prevailed. The fact that Huygens’s principle worked was not considered evidence that was direct enough to prove that light is a wave. The acceptance of the wave character of light came many years later when, in 1801, the English physicist and physician Thomas Young (1773–1829) did his now-classic double slit experiment (see Figure 1 ).

Why do we not ordinarily observe wave behavior for light, such as observed in Young’s double slit experiment? First, light must interact with something small, such as the closely spaced slits used by Young, to show pronounced wave effects. Furthermore, Young first passed light from a single source (the Sun) through a single slit to make the light somewhat coherent. By coherent , we mean waves are in phase or have a definite phase relationship. Incoherent means the waves have random phase relationships. Why did Young then pass the light through a double slit? The answer to this question is that two slits provide two coherent light sources that then interfere constructively or destructively. Young used sunlight, where each wavelength forms its own pattern, making the effect more difficult to see. We illustrate the double slit experiment with monochromatic (single [latex]{\lambda}[/latex]) light to clarify the effect. Figure 2 shows the pure constructive and destructive interference of two waves having the same wavelength and amplitude.

When light passes through narrow slits, it is diffracted into semicircular waves, as shown in Figure 3 (a). Pure constructive interference occurs where the waves are crest to crest or trough to trough. Pure destructive interference occurs where they are crest to trough. The light must fall on a screen and be scattered into our eyes for us to see the pattern. An analogous pattern for water waves is shown in Figure 3 (b). Note that regions of constructive and destructive interference move out from the slits at well-defined angles to the original beam. These angles depend on wavelength and the distance between the slits, as we shall see below.

To understand the double slit interference pattern, we consider how two waves travel from the slits to the screen, as illustrated in Figure 4 . Each slit is a different distance from a given point on the screen. Thus different numbers of wavelengths fit into each path. Waves start out from the slits in phase (crest to crest), but they may end up out of phase (crest to trough) at the screen if the paths differ in length by half a wavelength, interfering destructively as shown in Figure 4 (a). If the paths differ by a whole wavelength, then the waves arrive in phase (crest to crest) at the screen, interfering constructively as shown in Figure 4 (b). More generally, if the paths taken by the two waves differ by any half-integral number of wavelengths [[latex]{(1/2) \;\lambda}[/latex], [latex]{(3/2) \;\lambda}[/latex], [latex]{(5/2) \;\lambda}[/latex], etc.], then destructive interference occurs. Similarly, if the paths taken by the two waves differ by any integral number of wavelengths ([latex]{\lambda}[/latex], [latex]{2 \lambda}[/latex], [latex]{3 \lambda}[/latex], etc.), then constructive interference occurs.

Take-Home Experiment: Using Fingers as Slits

Look at a light, such as a street lamp or incandescent bulb, through the narrow gap between two fingers held close together. What type of pattern do you see? How does it change when you allow the fingers to move a little farther apart? Is it more distinct for a monochromatic source, such as the yellow light from a sodium vapor lamp, than for an incandescent bulb?

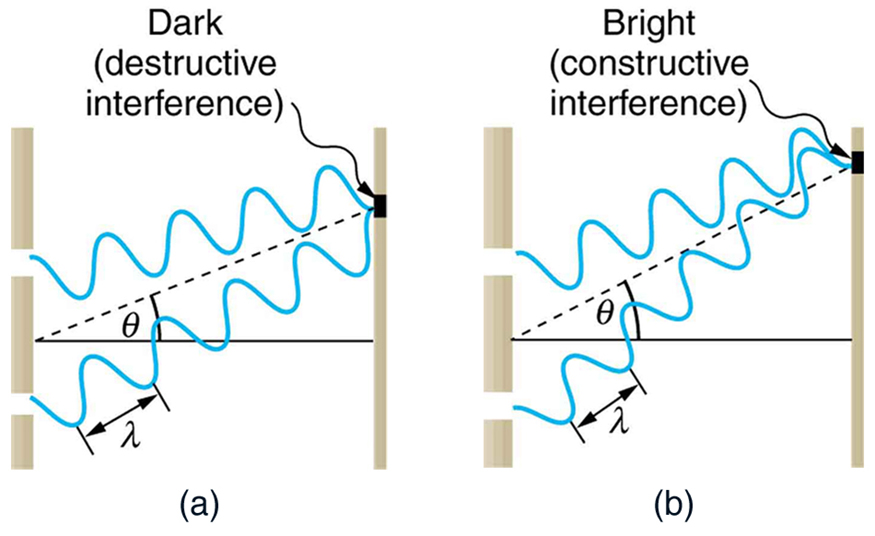
Figure 5 shows how to determine the path length difference for waves traveling from two slits to a common point on a screen. If the screen is a large distance away compared with the distance between the slits, then the angle [latex]{\theta}[/latex] between the path and a line from the slits to the screen (see the figure) is nearly the same for each path. The difference between the paths is shown in the figure; simple trigonometry shows it to be [latex]{d \;\text{sin} \;\theta}[/latex], where [latex]{d}[/latex] is the distance between the slits. To obtain constructive interference for a double slit , the path length difference must be an integral multiple of the wavelength, or

Similarly, to obtain destructive interference for a double slit , the path length difference must be a half-integral multiple of the wavelength, or

where [latex]{\lambda}[/latex] is the wavelength of the light, [latex]{d}[/latex] is the distance between slits, and [latex]{\theta}[/latex] is the angle from the original direction of the beam as discussed above. We call [latex]{m}[/latex] the order of the interference. For example, [latex]{m = 4}[/latex] is fourth-order interference.

The equations for double slit interference imply that a series of bright and dark lines are formed. For vertical slits, the light spreads out horizontally on either side of the incident beam into a pattern called interference fringes, illustrated in Figure 6 . The intensity of the bright fringes falls off on either side, being brightest at the center. The closer the slits are, the more is the spreading of the bright fringes. We can see this by examining the equation

For fixed [latex]{\lambda}[/latex] and [latex]{m}[/latex], the smaller [latex]{d}[/latex] is, the larger [latex]{\theta}[/latex] must be, since [latex]{\text{sin} \;\theta = m \lambda / d}[/latex].

This is consistent with our contention that wave effects are most noticeable when the object the wave encounters (here, slits a distance [latex]{d}[/latex] apart) is small. Small [latex]{d}[/latex] gives large [latex]{\theta}[/latex], hence a large effect.

Example 1: Finding a Wavelength from an Interference Pattern

Suppose you pass light from a He-Ne laser through two slits separated by 0.0100 mm and find that the third bright line on a screen is formed at an angle of [latex]{10.95 ^{\circ}}[/latex] relative to the incident beam. What is the wavelength of the light?

The third bright line is due to third-order constructive interference, which means that [latex]{m = 3}[/latex]. We are given [latex]{d = 0.0100 \;\text{mm}}[/latex] and [latex]{\theta = 10.95^{\circ}}[/latex]. The wavelength can thus be found using the equation [latex]{d \;\text{sin} \;\theta = m \lambda}[/latex] for constructive interference.

The equation is [latex]{d \;\text{sin} \;\theta = m \lambda}[/latex]. Solving for the wavelength [latex]{\lambda}[/latex] gives

Substituting known values yields

To three digits, this is the wavelength of light emitted by the common He-Ne laser. Not by coincidence, this red color is similar to that emitted by neon lights. More important, however, is the fact that interference patterns can be used to measure wavelength. Young did this for visible wavelengths. This analytical technique is still widely used to measure electromagnetic spectra. For a given order, the angle for constructive interference increases with [latex]{\lambda}[/latex], so that spectra (measurements of intensity versus wavelength) can be obtained.

Example 2: Calculating Highest Order Possible

Interference patterns do not have an infinite number of lines, since there is a limit to how big [latex]{m}[/latex] can be. What is the highest-order constructive interference possible with the system described in the preceding example?

Strategy and Concept

The equation [latex]{d \;\text{sin} \;\theta = m \lambda \; (\text{for} \; m = 0, \; 1, \; -1, \; 2, \; -2, \; \dots)}[/latex] describes constructive interference. For fixed values of [latex]{d}[/latex] and [latex]{\lambda}[/latex], the larger [latex]{m}[/latex] is, the larger [latex]{\text{sin} \;\theta}[/latex] is. However, the maximum value that [latex]{\text{sin} \;\theta}[/latex] can have is 1, for an angle of [latex]{90 ^{\circ}}[/latex]. (Larger angles imply that light goes backward and does not reach the screen at all.) Let us find which [latex]{m}[/latex] corresponds to this maximum diffraction angle.

Solving the equation [latex]{d \;\text{sin} \;\theta = m \lambda}[/latex] for [latex]{m}[/latex] gives

Taking [latex]{\text{sin} \;\theta = 1}[/latex] and substituting the values of [latex]{d}[/latex] and [latex]{\lambda}[/latex] from the preceding example gives

Therefore, the largest integer [latex]{m}[/latex] can be is 15, or

The number of fringes depends on the wavelength and slit separation. The number of fringes will be very large for large slit separations. However, if the slit separation becomes much greater than the wavelength, the intensity of the interference pattern changes so that the screen has two bright lines cast by the slits, as expected when light behaves like a ray. We also note that the fringes get fainter further away from the center. Consequently, not all 15 fringes may be observable.

Section Summary

• Young’s double slit experiment gave definitive proof of the wave character of light.
• An interference pattern is obtained by the superposition of light from two slits.
• There is constructive interference when [latex]{d \;\text{sin} \;\theta = m \lambda \;(\text{for} \; m = 0, \; 1, \; -1, \;2, \; -2, \dots)}[/latex], where [latex]{d}[/latex] is the distance between the slits, [latex]{\theta}[/latex] is the angle relative to the incident direction, and [latex]{m}[/latex] is the order of the interference.
• There is destructive interference when [latex]{d \;\text{sin} \;\theta = (m+ \frac{1}{2}) \lambda}[/latex] (for [latex]{m = 0, \; 1, \; -1, \; 2, \; -2, \; \dots}[/latex]).

Conceptual Questions

1: Young’s double slit experiment breaks a single light beam into two sources. Would the same pattern be obtained for two independent sources of light, such as the headlights of a distant car? Explain.

2: Suppose you use the same double slit to perform Young’s double slit experiment in air and then repeat the experiment in water. Do the angles to the same parts of the interference pattern get larger or smaller? Does the color of the light change? Explain.

3: Is it possible to create a situation in which there is only destructive interference? Explain.

4:   Figure 7 shows the central part of the interference pattern for a pure wavelength of red light projected onto a double slit. The pattern is actually a combination of single slit and double slit interference. Note that the bright spots are evenly spaced. Is this a double slit or single slit characteristic? Note that some of the bright spots are dim on either side of the center. Is this a single slit or double slit characteristic? Which is smaller, the slit width or the separation between slits? Explain your responses.

Problems & Exercises

2: Calculate the angle for the third-order maximum of 580-nm wavelength yellow light falling on double slits separated by 0.100 mm.

3: What is the separation between two slits for which 610-nm orange light has its first maximum at an angle of [latex]{30.0 ^{\circ}}[/latex]?

4: Find the distance between two slits that produces the first minimum for 410-nm violet light at an angle of [latex]{45.0 ^{\circ}}[/latex].

5: Calculate the wavelength of light that has its third minimum at an angle of [latex]{30.0 ^{\circ}}[/latex] when falling on double slits separated by [latex]{3.00 \;\mu \text{m}}[/latex]. Explicitly, show how you follow the steps in Chapter 27.7 Problem-Solving Strategies for Wave Optics .

6: What is the wavelength of light falling on double slits separated by [latex]{2.00 \;\mu \text{m}}[/latex] if the third-order maximum is at an angle of [latex]{60.0 ^{\circ}}[/latex]?

7: At what angle is the fourth-order maximum for the situation in Problems & Exercises 1 ?

8: What is the highest-order maximum for 400-nm light falling on double slits separated by [latex]{25.0 \;\mu \text{m}}[/latex]?

9: Find the largest wavelength of light falling on double slits separated by [latex]{1.20 \;\mu \text{m}}[/latex] for which there is a first-order maximum. Is this in the visible part of the spectrum?

10: What is the smallest separation between two slits that will produce a second-order maximum for 720-nm red light?

11: (a) What is the smallest separation between two slits that will produce a second-order maximum for any visible light? (b) For all visible light?

12: (a) If the first-order maximum for pure-wavelength light falling on a double slit is at an angle of [latex]{10.0^{\circ}}[/latex], at what angle is the second-order maximum? (b) What is the angle of the first minimum? (c) What is the highest-order maximum possible here?

13:   Figure 8 shows a double slit located a distance [latex]{x}[/latex] from a screen, with the distance from the center of the screen given by [latex]{y}[/latex]. When the distance [latex]{d}[/latex] between the slits is relatively large, there will be numerous bright spots, called fringes. Show that, for small angles (where [latex]{\text{sin} \;\theta \approx \theta}[/latex], with [latex]{\theta}[/latex] in radians), the distance between fringes is given by [latex]{\Delta y = x \lambda /d}[/latex].

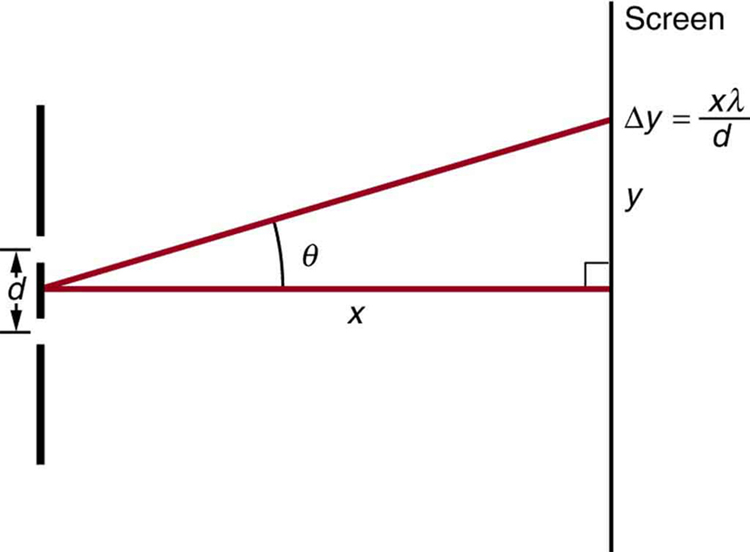
14: Using the result of the problem above, calculate the distance between fringes for 633-nm light falling on double slits separated by 0.0800 mm, located 3.00 m from a screen as in Figure 8 .

15: Using the result of the problem two problems prior, find the wavelength of light that produces fringes 7.50 mm apart on a screen 2.00 m from double slits separated by 0.120 mm (see Figure 8 ).

1:  [latex]{0.516 ^{\circ}}[/latex]

3:  [latex]{1.22 \times 10^{-6} \;\text{m}}[/latex]

7: [latex]{2.06 ^{\circ}}[/latex]

9: 1200 nm (not visible)

11: (a) 760 nm

(b) 1520 nm

13: For small angles [latex]{\text{sin} \;\theta - \;\text{tan} \;\theta \approx \theta}[/latex] (in radians).

For two adjacent fringes we have,

Subtracting these equations gives

College Physics Copyright © August 22, 2016 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Request a Demo
• Get A Quote
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Lab Equipment
• Lab Procedures
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Chemical Reactions Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Bond Energy and Reactions Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Task Tracker Directions
• Conceptual Physics Course
• On-Level Physics Course
• Honors Physics Course
• Chemistry Concept Builders
• All Chemistry Resources
• Users Voice
• Tasks and Classes
• Webinars and Trainings
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• Measurement and Calculations
• Elements, Atoms, and Ions
• Compounds,Names, and Formulas
• The Modern Atomic Model
• Chemical Bonding
• The Mole and its Applications
• Chemical Reactions
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Solution Guide Corrections
• Motion in One Dimension
• Work, Energy and Power
• Chemistry of Matter
• Measurement and the Metric System
• Early Atomic Models
• Names and Formulas
• The Modern Model of the Atom
• Algebra Based On-Level Physics
• Honors Physics
• Conceptual Physics
• Other Tools
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law

Young's Experiment

• Anatomy of a Two-Point Source Interference Pattern
• The Path Difference
• Young's Equation
• Young's Experiment
• Other Applications of Two-Point Source Interference

Today's classroom version of the same experiment is typically performed using a laser beam as the source. Rather than using a note card to split the single beam into two coherent beams, a carbon-coated glass slide with two closely spaced etched slits is used. The slide with its slits is most commonly purchased from a manufacturer who provides a measured value for the slit separation distance - the d value in Young's equation. Light from the laser beam diffracts through the slits and emerges as two separate coherent waves. The interference pattern is then projected onto a screen where reliable measurements can be made of L and y for a given bright spot with order value m . Knowing these four values allows a student to determine the value of the wavelength of the original light source.

To illustrate some typical results from this experiment and the subsequent analysis, consider the sample data provided below for d, y, L and m.

(Note: AN 0 = central antinode and AN 4 = fourth antinode)  

The determination of the wavelength demands that the above values for d, y, L and m be substituted into Young's equation.

Careful inspection of the units of measurement is always advisable. The sample data here reveal that each measured quantity is recorded with a different unit. Before substituting these measured values into the above equation, it is important to give some thought to the treatment of units. One means of resolving the issue of nonuniform units is to simply pick a unit of length and to convert all quantities to that unit. If doing so, one might want to pick a unit that one of the data values already has so that there is one less conversion. A wise choice is to choose the meter as the unit to which all other measured values are converted. Since there are 1000 millimeters in 1 meter, the 0.250 mm is equivalent to 0.000250 meter. And since there are 100 centimeters in 1 meter, the 10.2 cm is equivalent to 0.102 m. Thus, the new values of d, y and L are:

While the conversion of all the data to the same unit is not the only means of treating such measured values, it might be the most advisable - particularly for those students who are less at ease with such conversions.

Now that the issue regarding the units of measurement has been resolved, substitution of the measured values into Young's equation can be performed.

λ  = 6.52 x 10 -7 m

As is evident here, the wavelength of visible light is rather small. For this reason wavelength is often expressed using the unit nanometer, where 1 meter is equivalent to 10 9 nanometers. Multiplying by 10 9 will convert the wavelength from meters to nanometers (abbreviated nm).

We Would Like to Suggest ...

Check Your Understanding

1. The diagram below depicts the results of Young's Experiment. The appropriate measurements are listed on the diagram. Use these measurements to determine the wavelength of light in nanometers. (GIVEN: 1 meter = 10 9 nanometers)

Answer: 657 nm

First, identify known values in terms of their corresponding variable symbol:

L = 10.2 m = 1020 cm y = 22.5 cm m = 10 d = 0.298 mm = 0.0298 cm

(Note: m was chosen as 10 since the y distance corresponds to the distance from the 5th bright band on one side of the central band and the 5th bright band on the other side of the central band.)

Then convert all known values to an identical unit. In this case, cm has been chosen as the unit to use. The converted values are listed in the table above.

Substitute all values into Young's equation and perform calculation of the wavelength. The unit of wavelength is cm.

λ = y • d / ( m • L) λ = ( 22.5 cm ) • ( 0.0298 cm ) / [ ( 10 ) • ( 1020 cm ) ] λ = 6.57 x 10 -5 cm

Finally convert to nanometers using a conversion factor. If there are 10 9 nm in 1 meter, then there must be 10 7 nm in the smaller centimeter.

λ = ( 6.57 x 10 -5 cm ) • ( 10 7 nm / 1 cm ) = 657 nm

2. A student uses a laser and a double-slit apparatus to project a two-point source light interference pattern onto a whiteboard located 5.87 meters away. The distance measured between the central bright band and the fourth bright band is 8.21 cm. The slits are separated by a distance of 0.150 mm. What would be the measured wavelength of light?

Answer: 524 nm

L = 5.87 m = 587 cm y = 8.21 cm m = 4 d = 0.150 mm = 0.0150 cm

λ = y • d / ( m • L) λ = ( 8.21 cm ) • ( 0.0150 cm ) / [ ( 4 ) • ( 587 cm ) ] λ = 5.24 x 10 -5 cm

λ = ( 5.24 x 10 -5 cm ) • ( 10 7 nm / 1 cm ) = 524 nm

3. The analysis of any two-point source interference pattern and a successful determination of wavelength demands an ability to sort through the measured information and equating the values with the symbols in Young's equation. Apply your understanding by interpreting the following statements and identifying the values of y, d, m and L. Finally, perform some conversions of the given information such that all information share the same unit.

This question simply asks to equate the stated information with the variables of Young's equation and to perform conversions such that all information is in the same unit.

(Note that m = 4.5 represents the fifth nodal position or dark band from the central bright band. Also note that the given values have been converted to cm.)

b. An interference pattern is produced when light is incident upon two slits that are 50.0 micrometers apart. The perpendicular distance from the midpoint between the slits to the screen is 7.65 m. The distance between the two third-order antinodes on opposite sides of the pattern is 32.9 cm.

This question simply asks to equate the stated information with the variables of Young's equation and to perform conversions such that all information is in the same unit. 

(Note that m = 6 corresponds to six spacings. There are three spacings between the central antinode and the third antinode. The stated distance is twice as far so the m value must be doubled. Also note that the given values have been converted to cm. There are 10 6 µm in one meter; so there are 10 4 µm in one centimeter.)

c. The fourth nodal line on an interference pattern is 8.4 cm from the first antinodal line when the screen is placed 235 cm from the slits. The slits are separated by 0.25 mm.

 ( Note that the fourth nodal line is assigned the order value of 3.5. Also note that the given values have been converted to cm.)

d. Two sources separated by 0.500 mm produce an interference pattern 525 cm away. The fifth and the second antinodal line on the same side of the pattern are separated by 98 mm.

  ( Note that there are three spacings between the second and the fifth bright bands. Since all spacings are the same distance apart, the distance between the second and the fifth bright bands would be the same as the distance between the central and the third bright bands. Thus, m = 3. Also note that the given values have been converted to cm.)

e. Two slits that are 0.200 mm apart produce an interference pattern on a screen such that the central maximum and the 10th bright band are distanced by an amount equal to one-tenth the distance from the slits to the screen.

 ( Note that there are 10 spacings between the central anti-node and the tenth bright band or tenth anti-node. And observe that they do not state the actual values of L and y; the value of y is expressed in terms of L. )

f. The fifth antinodal line and the second nodal line on the opposite side of an interference pattern are separated by a distance of 32.1 cm when the slits are 6.5 m from the screen. The slits are separated by 25.0 micrometers.

 ( Note that there are five spacings between the central anti-node and the fifth anti-node. And there are 1.5 spacings from the central anti-node in the opposite direction out to the second nodal line. Thus, m = 6.5. Also note that the given values have been converted to cm. There are 10 6 µm in one meter; so there are 10 4 µm in one centimeter.)

g. If two slits 0.100 mm apart are separated from a screen by a distance of 300 mm, then the first-order minimum will be 1 cm from the central maximum.

  ( Note that a the first-order minimum is a point of minimum brightness or a nodal position. The first-order minimum is the first nodal position and is thus the m = 0.5 node. Also note that the given values have been converted to cm. )

h. Consecutive bright bands on an interference pattern are 3.5 cm apart when the slide containing the slits is 10.0 m from the screen. The slit separation distance is 0.050 mm.

   ( Note that the spacing between adjacent bands is given. This distance is equivalent with the distance from the central bright band to the first antinode. Thus, m = 1. Also note that the given values have been converted to cm. )